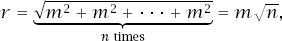Authors: Julian Havil
Nonplussed! (30 page)
Figure 11.5.
Parrondo’s Paradox.
We could take, for example,
p
= 0.45,
p
1
= 0.01,
p
2
= 0.90,
γ
= 0.5 to give
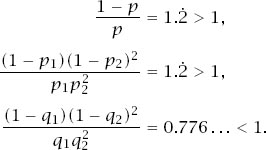
A simulation of the play of the games is given in
figure 11.5
. The plot is the average fortune over 1000 trials when each of game A, B and C is played up to 100 times with the probabilities given above.
Exactly What Is Happening?
The choices for the probabilities may seem arbitrary (and to some extent they are), but we can see further into the matter if we look at a plot of the function
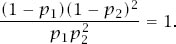
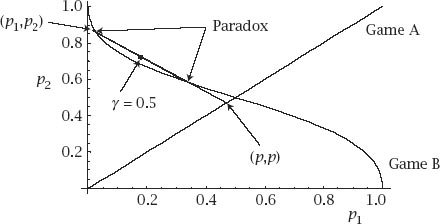
Figure 11.6.
The paradox exposed.
If we consider this as
p
2
being a function of
p
1
and write that function explicitly, we have
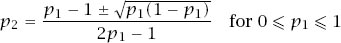
and since 0 ≤
p
2
≤ 1 we are interested only in
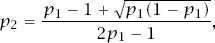
which is the curve in
figure 11.6
. Its behaviour at
p
1
= 0.5 is defined by continuity.
Points on and below the curve represent pairs
p
1
,
p
2
for which game B is losing. The diagonal straight line is
p
2
=
p
1
and so points on it represent choices of
p
in game A; below and on the intersection point (0.5,0.5) game A is losing and above it game A is winning.
Now recall the probabilities
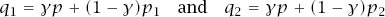
of game C winning. If we write these equations as
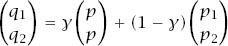
and let
γ
vary, we can see that the pairs (
q
1
,
q
2
) lie on the straight line joining (
p
,
p
) to (
p
1
,
p
2
). The paradox exists when the points (
p
,
p
) and (
p
1
,
p
2
) are chosen so that the line passes above the curve, since game B for these values (that is, game C) is winning. It is the convexity of the curve that allows the paradox to exist. The third line joins the two points defined by our choice of probabilities above and marked on it is the point corresponding to our choice of
γ
= 0.5.
It may be a little contrived, but here we have a procedure for making a winning game out of two losing games. Since the idea was introduced, there have been many examples of real-world manifestations of the fact that a combination of two negative characteristics can result in a positive one. To demonstrate the diversity that exists, in 2000 in the
New York Times
, Dr Sergei Maslov from Brookhaven National Laboratory was reported to have shown that if an investor simultaneously shared capital between two losing stock portfolios, capital would increase rather than decrease; Brooke Buckley, an undergraduate student from Eastern Kentucky University, mentions in her thesis the well-known fact in agriculture ‘that both sparrows and insects can eat all the crops. However, by having a combination of sparrows and insects, a healthy crop is harvested.’
HYPERDIMENSIONS
I recall a lecture by John Glenn, the first American to go into orbit. When asked what went through his mind while he was crouched in the rocket nose-cone, awaiting blast-off, he replied, ‘I was thinking that the rocket has 20,000 components, and each was made by the lowest bidder.’
Martin Rees
Some dimensionally dependent phenomena seem reasonable. Take, for instance, the idea of a random walk. In one dimension this means that we start at the origin and move to the left or the right with equal probability; in two dimensions we have four equally probable directions in which we can walk; in both cases it can be shown that the probability of eventually returning to the origin is 1; we cannot, in theory, get lost. As the dimension increases, so we might reasonably think are the chances of getting lost, never to return to the origin, increase, and so they do. In three dimensions the probability of our return is only about 0.34 and in
n
dimensions, where
n
is large, that probability is about 1/2
n
. But it does not take much investigation into hyper-dimensions to cause our intuition to be confounded.
Figure 12.1.
Touching circles.
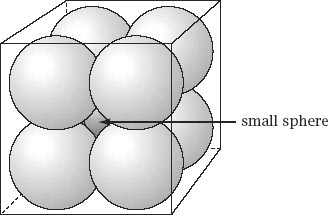
Figure 12.2.
Touching spheres.
A Strange Phenomenon
Figure 12.1
shows a 4 × 4 square inside of which is embedded four touching circles, each of radius 1. It also shows a smaller fifth circle of radius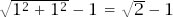
inscribed at the centre of the square, itself touching all four circles. There is nothing surprising here.
Figure 12.2
shows the equivalent situation in three dimensions. Inside a cube of side 4 are embedded eight touching spheres, each of radius 1, and once again there is room for a smaller, extra sphere which touches all eight, this time its radius is
. Again, this is self-evident.
It is also self-evident that in both cases the central circle or sphere is contained in the surrounding square or cube.
Now suppose that we move from two to three to
n
dimensions and consider an
n
-dimensional hypercube, in which hyper-spheres are inscribed. The definitions of these objects are reasonable enough.
An
n
-dimensional hypercube of side
L
(with one vertex at the origin) is the set of all
n
-tuples {
x
1
,
x
2
,
x
3
,…,
x
n
}, where
x
r
{0,
L
}: the figure has 2
n
vertices (and we can embed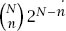
of them in (
N
≥
n
)-dimensional space).
An
n
-dimensional hypersphere of radius
R
is the set of all
n
-tuples {
x
1
,
x
2
,
x
3
,…,
x
n
} such that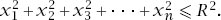
Currently, we are interested in the case
L
= 4 and if we carry out the natural calculation for the radius of the small, inscribed hypersphere using the generalized Pythagoras Theorem, we get
>
Putting
n
= 2 or 3 gives us the previous results, but reflect on the fact that the distance from the centre of the hypercube to any of its sides is always precisely 2 units. Now consider the situation when
n
= 9; the radius of the inner, touching hypersphere
, which must mean that it touches the sides of the hypercube, and, when
n
> 9, it protrudes outside it!
Furthermore, using Pythagoras’s Theorem on an
n
-dimensional hypercube of side
m
, the length of the ‘space diagonal’ is
