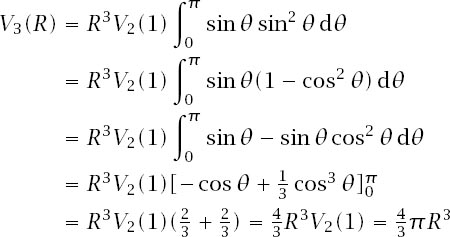Nonplussed! (31 page)

so if we wanted to place a stick of length
L
into the hypercube we would require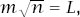
, which means that, as the dimension increases, the side of the hypercube needed to contain the stick diminishes. For example, a hypercube of side 1 metre of dimension 100 could contain a stick of length 10 metres; one of dimension 2.25 × 10
⁶
could contain a stick of length the metric mile (1500 metres).

Extrapolating from what is evident from our three-dimensional perspective to what is logically, but uncomfortably, true in hyperspace forms the substance of this chapter, and also of a famous piece of mathematical literature.

The Literary Dimension

The little Hexagon meditated on this a while and then said to me:

‘But you have been teaching me to raise numbers to the third power: I suppose three-to-the-third must mean something in Geometry; what does it mean?’

‘Nothing at all,’ replied I, ‘not at least in Geometry; for Geometry has only Two Dimensions.’

And then I began to show the boy how a Point by moving through a length of three inches makes a Line of three inches, which may be represented by three; and how a Line of three inches, moving parallel to itself through a length of three inches, makes a Square of three inches every way, which may be represented by three-to-the-second. Upon this, my Grandson, again returning to his former suggestion, took me up rather suddenly and exclaimed,

‘Well, then, if a Point by moving three inches, makes a Line of three inches represented by three; and if a straight Line of three inches, moving parallel to itself, makes a Square of three inches every way, represented by three-to-the-second; it must be that a Square of three inches every way, moving somehow parallel to itself (but I don’t see how) must make something else (but I don’t see what) of three inches every way – and this must be represented by three-to-the-third.’

The dialogue originates from a conversation between a Square, the principal character of Edwin A. Abbott’s 1884 mathematical romance,
Flatland
(
http://www.gutenberg.org/dirs/etext94/flat11.txt
), and his gifted, regular-hexagonal grandson. In a dream the Square, an inhabitant of a two-dimensional world, had already failed to explain Flatland to the monarch of one-dimensional Lineland; now his grandson had challenged him to comprehend a dimension above that in which they both lived.

A little later, a stranger from Spaceland appeared first as a point, which became a small circle, and which grew continuously to a circle of greatest size, which diminished to a point and which disappeared altogether; incomprehensible to the Flat-landers, that stranger was a three-dimensional sphere which had passed through their two-dimensional world.

The earlier examples provided an elementary case in which our Spacelander perception is confounded and the remainder of this chapter concentrates on several other hyperdimensional results, which are at the very least exotic.

Volumes in Discrete Hyperdimensions

The volume of a hypercube of side
L
is very straightforward to calculate:
C
_n
(
L
) =
L
ⁿ
. In particular, we have that

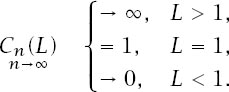
Now we will undertake the significantly greater challenge of finding
V
_n
(
X
), the volume of the
n
-dimensional hypersphere of radius
X
.

It is important to understand that this is related to the volume of the
n
-dimensional hypersphere of radius 1 by
V
_n
(
X
) =
X
ⁿ
V
_n
(1), since the transition from a hypersphere of radius 1 to one of radius
X
may be thought of as a uniform change of units in each of the dimensions; the rules of similarity dictate that the volume will change by the product of these changes.

To approach the problem of finding
V
_n
(
X
) we could naturally delve into the world of
n
-fold multiple integrals, but it is wise to avoid such esotericism. Instead, we will extend the use of Cavalieri’s Principle (
chapter 8
) from finding the volume of a sphere to that of our hypersphere.

The principle tells us that to find the volume of a solid, take an arbitrary (
x
) axis which runs through it and add the areas of the sections
A
(
x
) through the solid, perpendicular to this axis, as demonstrated in
figure 12.3
.

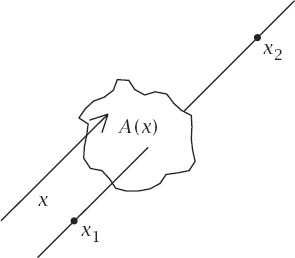
Figure 12.3.
Finding volume using Cavalieri’s Principle.

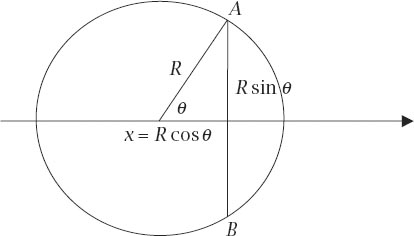
Figure 12.4.
A section of a three-dimensional sphere.

In symbols, the volume is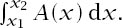
. Now apply this to our three-dimensional sphere, centred at the origin, and take the
x
-axis as the chosen axis.

Figure 12.4
gives a sectional view of the sphere with
A
(
x
) a circular section distant
x
=
R
cos
θ
from its centre and of diameter
AB
; the radius of the cross-section is therefore
R
sin
θ
. We then have

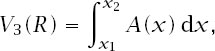
where

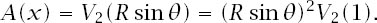
Since
x
=
R
cos
θ
we have d
x
/d
θ
= −
R
sin
θ
and can substitute

θ
for
x
in the integral to get

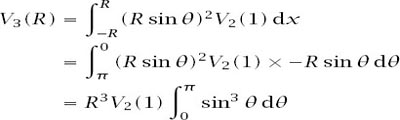
and the problem reduces to finding a standard integral.

The calculation continues as