Nonplussed! (32 page)
Authors: Julian Havil

noting that
V
2
(1) =
π
× 1
2
=
π
.
Having established a comfortingly familiar result, we will continue to find a general formula for the volume of the
n
-dimensional hypersphere,
V
n
(
R
), noting that
A
(
x
) will be the volume of an (
n
− 1)-dimensional hypersphere.
Following the same route, we get
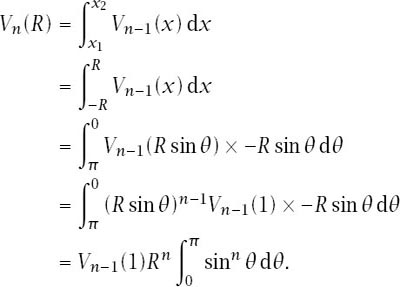
So
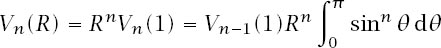
and we conclude that
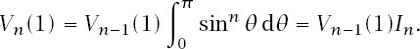
We have a recursive formula for
V
n
(1) which also involves the integral
I
n
and to derive an explicit formula we will first find an explicit formula for
I
n
and use it to chase down the
V
n
(1).
First, the
I
n
, which we attack in a standard way, using integration by parts to establish a reduction formula:
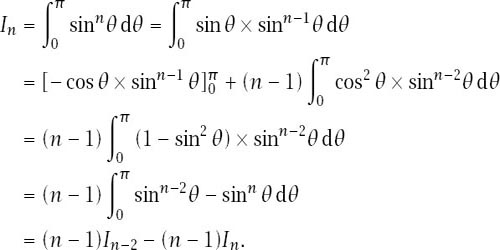
This means that
I
n
= ((
n
− 1)/
n
)
I
n−2
, which we can use to find explicit formulae for
I
n
, depending on whether
n
is even or odd.
For
n
even:
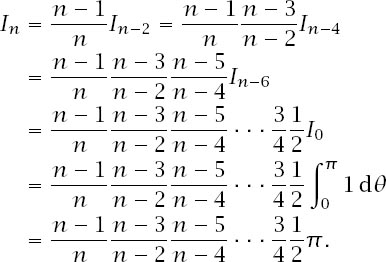
For
n
odd:
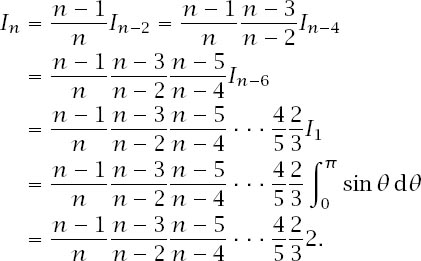
Now we use these to establish a connection between
I
n
and
I
n
−1
that is independent of the parity of
n
.
If
n
is even, it must be that
n
−1 is odd and we use the appropriate formulae to get
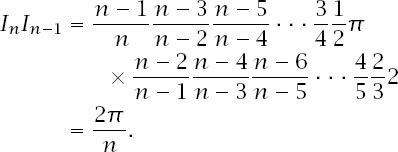
If
n
is odd, it must be that
n
− 1 is even and again we use the appropriate formulae to get
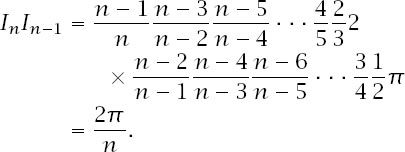
So, whatever the parity of
n
,
I
n
I
n
−1
= 2
π
/
n
.
Now recall that
V
n
(1) =
V
n
−1
(1)
I
n
and reuse the formula once on itself to get
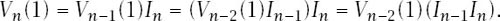
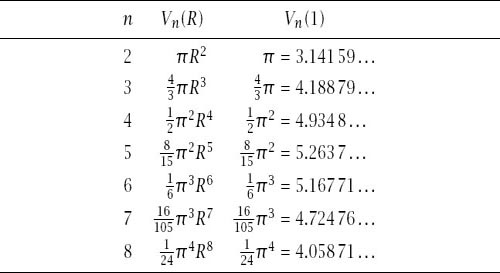
Table 12.1.
Volumes of hyperspheres.
Now we can say that
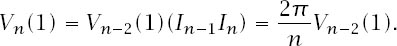
We have a simple reduction formula for the
V
n
(1) and we can chase it down, again depending on whether
n
is even or odd to get the answer:
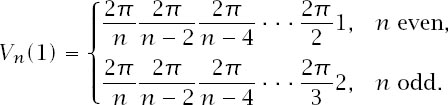
Of course, this means that
