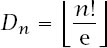Nonplussed! (14 page)

we can see why. The expansion is valid for all
x
and, in particular, for
x = -
1, and at this value the identity becomes

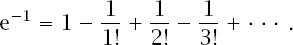
Of course, this is an infinite series and
p
_n
has only a finite number of terms but it provides a hint that e does appear in formulae for
D
_n
, and perhaps the nicest example of its type is

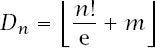
and so

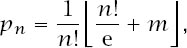
where
m
is any number such that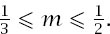

(Here, the
[·]
is the floor function defined by [
x
] = the greatest integer less than or equal to
x
.)

To see this, write

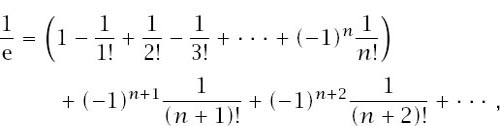
which means that

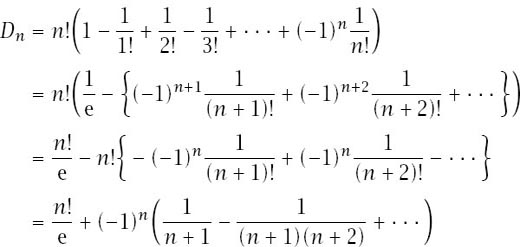
and pairing the terms after the first makes clear that

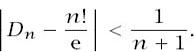
Now, if
n
is even, the above expression for
D
_n
shows that
D
_n
> n
!
/
e and so

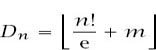
provided that

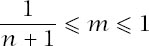
and since
n
≥2 we require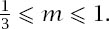

If
n
is odd,
D
_n
< n
!
/
e and now

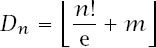
provided that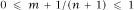
and this means that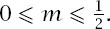

Take these two results together and we have the result. Of course, it can be convincingly argued that
m =
0 provides the nicest expression