Nonplussed! (15 page)
Authors: Julian Havil

and so
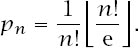
It can also be shown that
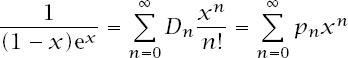
is a generating function for the
p
n
, but that is another story!
A Generalization
We have seen that derangements are permutations without a fixed point. The obvious generalization of this is to allow a specific number of fixed points, in which case we approach the general form of rencontres numbers
D
n
(k)
, the number of permutations of
n
objects which have precisely
k
fixed points,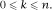 Since the work involved in finding an expression for
Since the work involved in finding an expression for
D
n
(k)
is now trivial, we may as well do just that. If we have
k
fixed points, which can be chosen in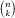 ways, we must have a derangement of the remaining
ways, we must have a derangement of the remaining
n - k
numbers and this can be achieved
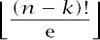
in ways. Thus
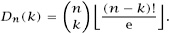
And these can be conveniently displayed as a triangular array,

with the numbers in the leftmost vertical column the number of derangements, of course.
This means that the probability that a permutation has exactly
k
fixed points is
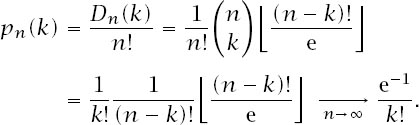
Summing this last expression from
k = 0 to
∞ gives the answer 1, essential for a probability distribution. And this has connections with moments of distributions, which have connections with Bell Numbers, and these with partitions – none of which we will enter into here!
1
Available at
www.rose-hulman.edu/mathjournal/archives/2003/vol4-n1/paper2/v4n1-2do.doc
.
CONWAY’S CHEQUERBOARD ARMY
Games are among the most interesting creations of the human mind, and the analysis of their structure is full of adventure and surprises.
James R. Newman
John Horton Conway is very hard to encapsulate. He is universally acknowledged as a world-class mathematician, a claim strongly substantiated by his occupation of the John von Neumann Chair of Mathematics at Princeton University. His vast ability and remarkable originality have caused him to contribute significantly to group theory, knot theory, number theory, coding theory and game theory (among other things); he is also the inventor of surreal numbers, which seem to be the ultimate extension of the number system and, most famous of all in popular mathematics, he invented the cellular automata game of Life. In
chapter 14
we will look at him putting fractions to mysterious use, but here we will be concerned with another cellular game, typically simple, and typically deep.
The Problem
Imagine an infinite, two-dimensional chequerboard divided in half by an infinite barrier, as in
figure 6.1
. Above the barrier the
horizontal levels are numbered as shown. Chequers are placed on the squares below the barrier and can move horizontally or vertically below it or above it by jumping over and removing an adjacent piece. The puzzle Conway associated with this simple situation is to find starting configurations entirely below the barrier which will allow a single chequer to reach a particular target level above the barrier. It’s very instructive to experiment with the pieces and, having done so,
figure 6.2
shows the minimal configurations required to reach levels 1 to 3; in each case the target square T is reached by a single chequer.

Figure 6.1.
The playing area
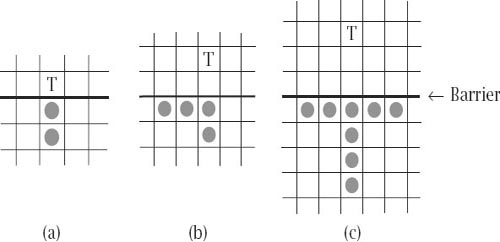
Figure 6.2.
Reaching (a) level 1, (b) level 2, (c) level 3
The minimal number of chequers needed to reach levels 1, 2 and 3 is then 2, 4 and 8, respectively. The answer for level 4 is more complicated and, in what might be thought of as our first
surprise,
figure 6.3
discloses that it is not 16 but a full 20 pieces that are needed to reach the target square T.
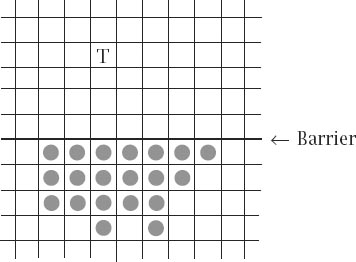
Figure 6.3.
Reaching level 4
Table 6.1.
The level/chequer-count comparison.

The second surprise, and the one which will occupy us for the rest of the chapter, is that level 5 is impossible to reach, no matter how many chequers are placed in whatever configuration below the barrier.
Table 6.1 summarizes the situation. The result is indeed surprising, but then so is Conway’s ingenious method of proof, which, apart from anything else, brings in the Golden Ratio.
The Solution
To start with, fix any target square T on level 5 and, relative to it, associate with every square a nonnegative integer power of the variable
x
, that power being the ‘chequerboard distance’
or ‘taxicab distance’ of the square from T. Such a distance is measured as the number of squares, measured horizontally and vertically from T, which gives rise to
figure 6.4
.
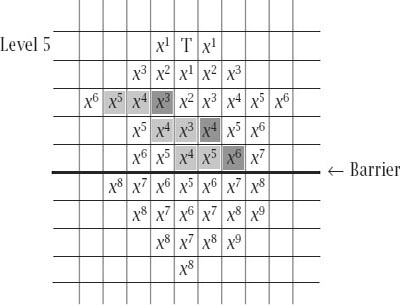
Figure 6.4.
The labelling of the squares
With this notation in place, every arrangement of chequer pieces, whether the initial configuration or the configuration at some later stage, can be represented by the polynomial formed by adding each of these powers of
x
together, for example, the starting positions to reach levels 1 to 4 might be represented by the polynomials
x
5
+x
6
,
x
5
+2
x
6
+x
7
,
x
5
+3
x
6
+3
x
7
+x
8
and
x
5
+ 3
x
6
+ 5
x
7
+ 6
x
8
+ 4
x
9
+ x
10
, respectively.
We now look at the effect of a move on the representing polynomial by realizing that, for this purpose, the choice of moves reduces to just three essentially different possibilities, which are characterized by the shaded cells in
figure 6.4
, where counters in the light grey squares are replaced by the counter in the dark grey square in each case. The general forms of these are

Any starting configuration will define a polynomial and, with every move that is made, that polynomial will change according to one of the three possibilities detailed above. The variable
x
is arbitrary and we are free to replace it with any value we wish and will look to do so by choosing a value (greater than 0) which will cause the numeric value of the polynomial to decrease in the second and third cases and remain unchanged in the first (this last is for later algebraic convenience) when this number is substituted into it. Since
x >
0, evidently
x
n
+ x
n-
1
> x
n
. If
x
n
+ x
n+
1
> x
n+
2
, we require that 1
+ x > x
2
and this means that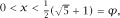 which brings about the promised appearance of the Golden Ratio.
which brings about the promised appearance of the Golden Ratio.
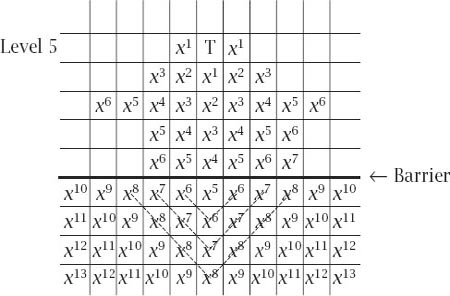
Figure 6.5.
The ultimate ‘polynomial’
