Nonplussed! (11 page)

And we now have a recurrence relation for
p
_n
, which we can most easily deal with by writing
q
_n
= p
_n
- p
_n-1
and chasing
down the expressions to get

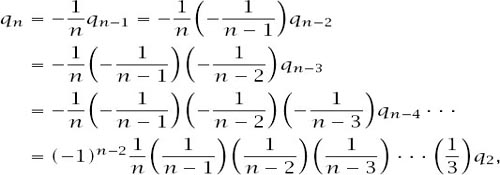
where

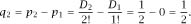
This means that we may write

tidying up the −1 term.

Now, if we write the expressions for
q
_n
explicitly, we get

and if we add the equations vertically we have, after almost complete cancellation on the right-hand side,

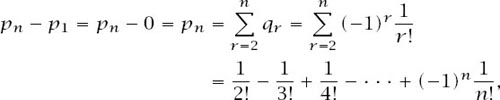
which can conveniently be written as

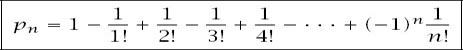
and we have the expression we seek.

Bernoulli’s Solution

The more powerful the mathematical tools used to prove a result, the shorter that proof might be expected to be and we should not ignore the significantly shorter attack which is based on the inclusion–exclusion principle. The general principle is discussed in appendix A and the eminent Nicholas Bernoulli used it to establish the formula for
D
_n
in the following way.

Using the inclusion–exclusion principle we have that

with the series finishing with the number 1, which is the total number of permutations fixing all
n
numbers. So,

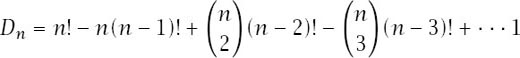
with the first part of each term the number of ways of choosing the numbers to be fixed and the second the number of permutations of what remains. Simplifying gives

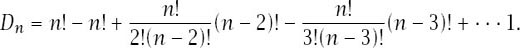
And so

and, once again,

The Final Proof

Following Heba Hathout’s article ‘The old hats problem’
¹
, we can count the
n
! ways of arranging the
n
objects by partitioning the ways into
n +
1 disjoint subsets
S
₀
,
S
₁
,
S
₂
,
…,S
_n
, where
S
_r
is the set of permutations in which there are exactly
n - r
fixed points, and we will write
N(S
_r
)
for the number of elements in
S
_r
. For example, if there are two fixed points, we have the subset of permutations
S
_n-2
with the two fixed points chosen in
possible ways: this means that