Nonplussed! (13 page)

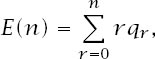
where
q
_r
is the probability of there being precisely
r
fixed values, which in our case is given by

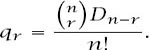
The argument is that of the previous section, with the
r
fixed values chosen in any of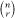
ways, leaving the remaining
(n -r)
numbers to be deranged. Our average value is, then,

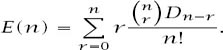
To evaluate the expression, we will change variable by writing
s = n - r
to get

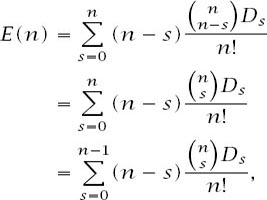
where the middle equality uses the symmetry of the binomial coefficients

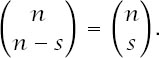
This means that

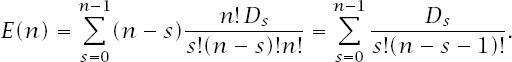
Multiplying both sides by
(n -
1
)
! results in

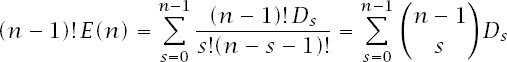
and this expression is just equation (1) on page 53 with
n
replaced by
n -
1. This means that
(n -
1
)
!
E(n) = (n -
1
)
! and so
E(n) =
1, independent of
n
.

Asymptotic Behaviour

We have, then, an attribute,
E(n)
, which is independent of the number of objects
n
and, if we look a little more closely at our earlier calculations, we can readily see that

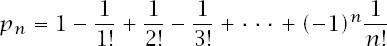
is also practically independent of
n
.

Put more positively, 1
- p
_n
is the probability of at least one match with
n
objects and simple computer calculations show that

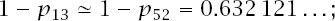
the two match to six decimal places, so it doesn’t really matter whether we play the original Montmort version of the game or the version considered by Euler.

Figure 5.1 shows the plot of 1
- p
_n
against
n
as a continuous function of
n
with that rapid convergence very evident. Put succinctly, there is about a 63% chance of at least one match, virtually independent of
n
, which is perhaps higher than one might imagine.

Finally, we will look a little more closely at the series which gives
p
_n
.

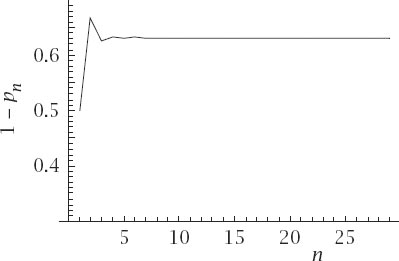
Figure 5.1.
Asymptotic behaviour

An Appearance of e

That expression

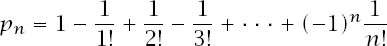
has a familiar look to it and if we examine the first
n
terms of the Taylor expansion of