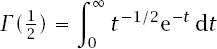Nonplussed! (33 page)
Authors: Julian Havil

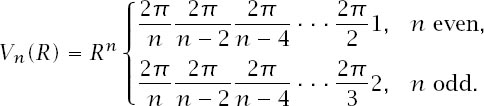
Table 12.1
lists the volumes for small values of
n
and we can see that the volume of the unit hypersphere peaks when
n
= 5 and that this maximal volume is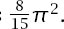 . A plot of
. A plot of
V
n
(1) against
n
is shown in
figure 12.5
, which indicates that the volume of the unit hypersphere is
decreasing
as
n
increases beyond 5, which appears very strange.
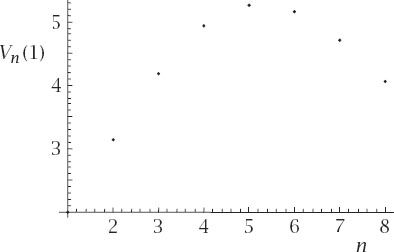
Figure 12.5.
Volume of the unit hypersphere compared with integer dimensions.
Volume in Continuous Hyperdimensions
The plotted points in
figure 12.5
are in such a regular pattern that it is natural to want to join them by a continuous curve, but doing so would force us to admit not only hyperdimensions but also nonintegral hyperdimensions. To approach this concept we need to rewrite the formulae for
V
n
(1) as below:
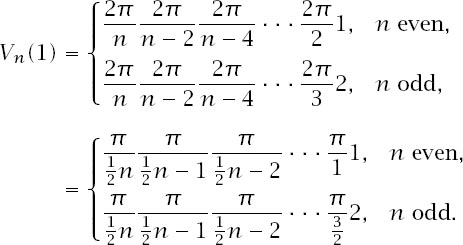
If
n
is even, the formula can be written in terms of factorials as
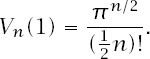
If
n
is odd,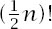 is not defined, but its generalization − the Gamma function
is not defined, but its generalization − the Gamma function
Γ
(
x
) − is. This function’s somewhat strange
definition is
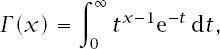
which is defined for
x
> 0 and which has two particular properties:
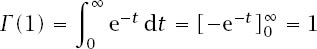
and
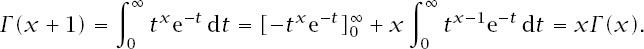
Together they characterize the factorial function, since, if
n
is a positive integer,
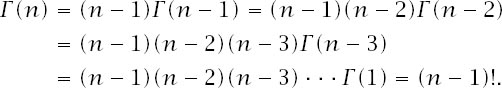
So, this peculiar function is indeed an extension of the factorial function, which is defined only for positive integers, to all
x
> 0. In fact, the above relationship, when rewritten as
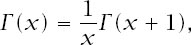
can be used to extend the idea of factorial to all numbers other than the negative integers and it is perfectly easy to extend the definition to complex numbers, but we will not concern ourselves with these excitements.
Note in particular that, if we accept a standard result that
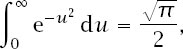
we have