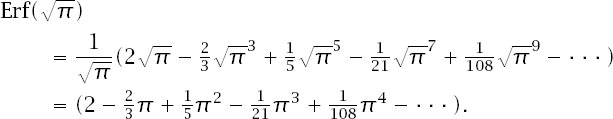Nonplussed! (36 page)
Authors: Julian Havil

which is altogether more challenging.
In fact, we can eliminate the Gamma function from the expression by using a result which connects it to another exotic function, the double factorial
N
!!, which is defined by
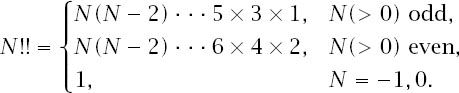
Using the standard properties of the Gamma function, it is not too hard to show that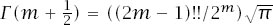 and this
and this
makes
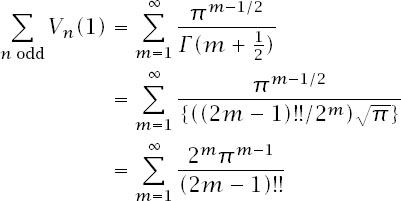
and it is easier still to show that (2
m
− 1)!! = (2
m
)!/(2
m
m
!), and this makes
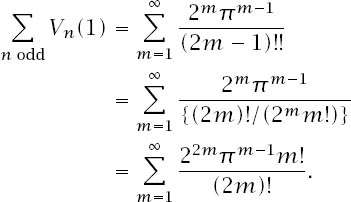
Now that we have the sum expressed in more elementary terms it is still far from obvious whether or not this series for odd
n
has a closed form, as the much simpler one did for even
n
. If we begin to write out the series explicitly, we have
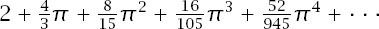
and those coefficients do not look particularly promising: a look in a standard mathematical handbook reveals nothing. In fact, the series does have a closed form, and to approach it we will engage in a common mathematical technique: the optimistic guess. Since e
π
appears in the expression for even
n
, it might just do so here and if it does the most reasonable form of its appearance would be
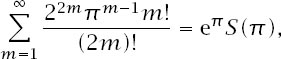
where
S
(
π
) is an infinite series in
π
. To find the form that this series must have, we need to rewrite the expression and expand both sides to compare coefficients:
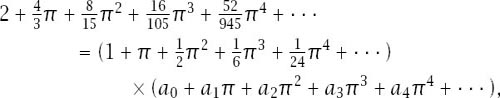
which leads to the sequence of coeffcients,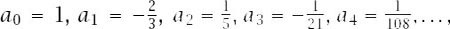 and our new series is
and our new series is
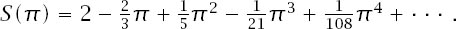
Even these coefficients promise little, but a second look in that mathematical handbook reveals the error function, Erf(
x
), with its series form
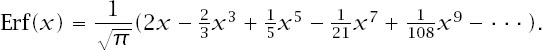
In fact, it is defined by
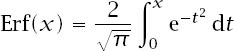
and comes from the theory of the normal distribution in statistics. Using the series expansion of e
-t
2
and integrating term by term results in the series form. Evaluate at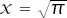 and we have precisely
and we have precisely