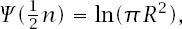Nonplussed! (37 page)
Authors: Julian Havil

Our
S
(
π
) is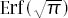 and therefore we have
and therefore we have
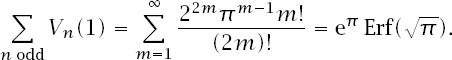
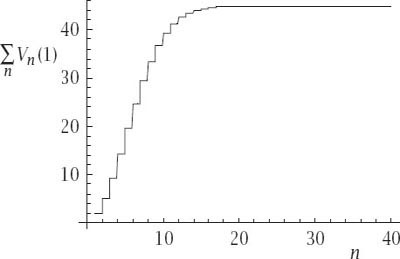
Figure 12.8.
Cumulative volumes of the unit hypercubes.
And this makes
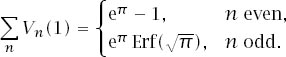
And the total volume
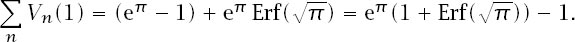
Of course, we have not rigorously proved this but from what we have seen it is at least feasible and evaluation of this exact expression to 44.999 326 089 382 855 366 … can only add to our confidence. It is the case that not too much extra analysis would prove it to be so.
In fact, we can see from
figure 12.8
, which shows a continuous plot of the cumulative sum, that the convergence is all but accomplished by the twentieth term.
Surface Area in Hyperdimensions
The surface area
A
n
(
R
) of the hypersphere whose volume is
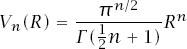
is simply the derivative of the expression with respect to
R
, so
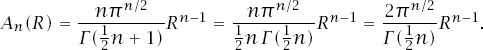
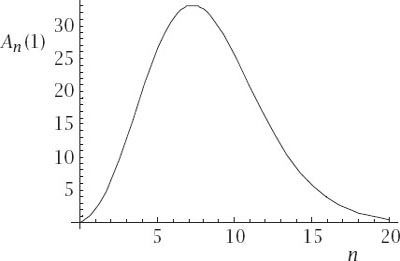
Figure 12.9.
Surface area of the unit hypersphere compared with continuous dimensions.
Table 12.3.
Surface areas of hyperspheres.

In particular,
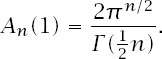
Table 12.3
lists the first few values of the hypersurface areas and indicates a peak at
n
= 7 for
A
n
(1).
figure 12.9
shows a plot of
A
n
(1) against a continuous
n
and indicates that the surface area of the hypersphere does peak at around
n
= 7 and that it also tends to 0 as
n
increases. Entirely similar calculations to the ones previously made show that for maximal
A
n
(1)
n
satisfies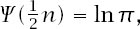 which tells us that the maximum is actually achieved when
which tells us that the maximum is actually achieved when
n
= 7.256 95 … and takes the value 33.1612 ….
Table 12.4.
Radius for maximal surface area.
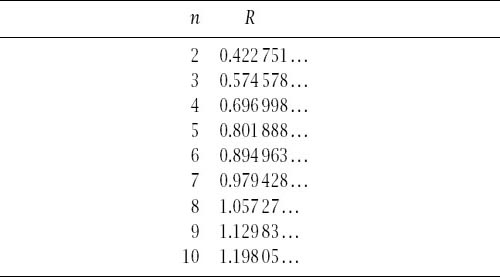
Almost repeating the argument for volume, if we wish to calculate the radius
R
of the hypersphere which has maximal surface area in each integral dimension, we use calculus on
A
n
(
R
) and this gives rise to the equation