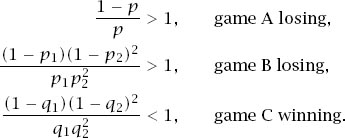Nonplussed! (29 page)

and substituting these expressions for
p
_3
r
+1
and
p
_3
r
−1
into equation (3) and simplifying gives

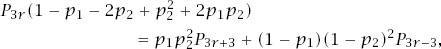
which can be rewritten as

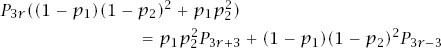
or

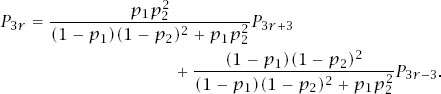
This may be messy but a careful look reveals that the sum of the coefficients is 1 and therefore that this has the form of equation (1) with

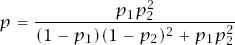
and
r
replaced by 3
r
.

We then have that

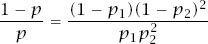
and so

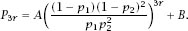
Exactly the same arguments as before, only this time with

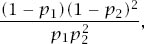
result in

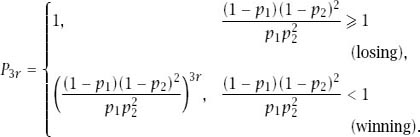
Repeat the same (rather tedious) working with
p
_3
r
+1
and
p
_3
r
+2
and we would get the equivalent expressions with 3
r
replaced by 3
r
+ 1 and 3
r
− 1, respectively, and we can compress the whole thing into what we have been seeking: an explicit expression for
P
_r
in terms of
r
, which is

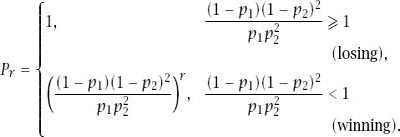
Notice that if we put
p
₁
=
p
₂
=
p
, the expression is exactly that of game A: game A is indeed a special case of game B.

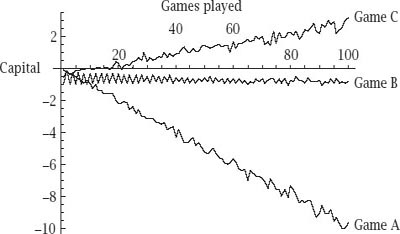
Now for the payoff, as we consider the composite game C.

Game C

Suppose that we play game A with a probability of γ and game B with a probability of 1 − γ. All depends on whether or not our current capital is a multiple of 3, as shown
figure 11.4
.

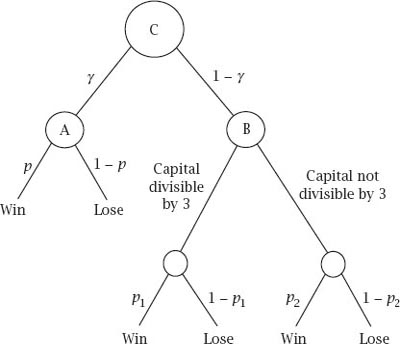
Figure 11.4.
Game C tree diagram.

If our capital is a multiple of 3, we will win with a probability
q
₁
=
γp
+ (1 −
γ
)
p
₁
and otherwise we win with a probability
q
₂
=
γp
+ (1 −
γ
)
p
₂
. This is an identical setup to game B with
q
replacing
p
, which means that

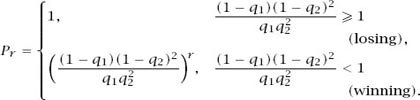
We will have a paradoxical position if