Nonplussed! (24 page)

Figure 9.10.
The initial tree diagram.

The left-hand column of
table 9.5
shows the eight possible choices that B can make. The middle column shows the corresponding choice that A should make in each case. If he makes that choice, the right-hand column shows the probability of A winning.

Compiling the column of odds takes a little effort and makes ample use of tree diagrams. We will consider the essentially different pairings separately, dealing in detail with the first of them.

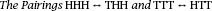
The first three tosses could be HHH, in which case B wins. Otherwise, a tail will appear among them and if this is the case, no matter how many more tails appear, A needs two heads and B still needs all three heads to win. A will assuredly get his two heads before B gets the three and it is just a mater of time before A wins. So, of the eight possibilities for the first three tosses, A will win on seven of them and so the probability of A winning is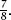

This is easy. Now to a slightly harder case.

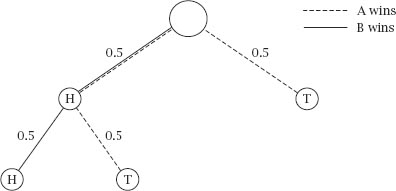
Figure 9.11.
The tree diagram pruned.

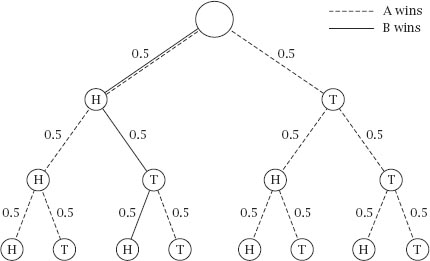
Figure 9.12.
The initial tree diagram.

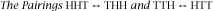
We will analyse the situation using a three-stage tree diagram, as shown in
figure 9.10
.

Figure 9.10 shows the two paths along which either A or B clearly wins, but a little thought allows us to prune the tree diagram. First, if the first toss is a T, no matter what happens subsequently, HH is needed to complete the sequence and these will
only start the sequence chosen by B; A must win; this means that the whole right-hand side of the tree diagram is a win for A. Further, if the first two tosses are HT, then A must win for the same reason. Lastly, if the first two tosses are HH, then B must win. The tree diagram reduces to
figure 9.11
.

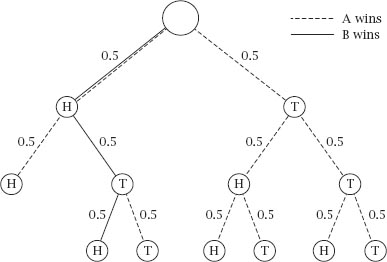
Figure 9.13.
The tree diagram pruned.

The probability that A wins is, then,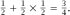

Finally, we need to deal with the middle four cases, and this is rather more subtle since the tree diagram does not fully resolve the situation in all cases.

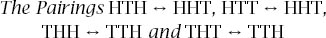
The three-stage tree diagram is shown in
figure 9.12

Once again, the branches can be trimmed, but by not so much this time. If the coin comes up HH, then A will assuredly win and similarly if it comes up THH. This results in
figure 9.13
.

To better analyse the remaining possibilities it is useful to add in an extra level, as in
figure 9.14
, where
p
is the probability that A wins.

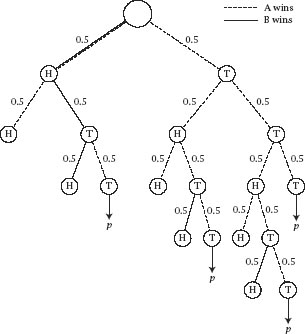
Figure 9.14.
The pruned tree diagram extended.

If we work through the branches from left to right, we have the expression

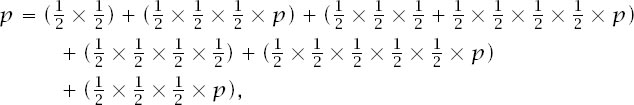
which makes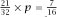
and so