Nonplussed! (22 page)
Authors: Julian Havil

and we have in our case
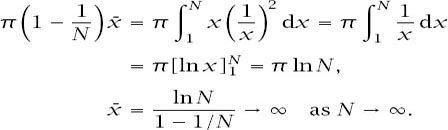
A Drinking Vessel
So, in 1643 Torricelli brought to the mathematical world a solid which has infinite surface area but finite volume. In 1658 Christiaan Huygens and René François de Sluze added to the mathematical unease of the time by reversing the conditions: their solid has finite surface area and infinite volume.
We will not consider their arguments or more modern ones to establish the fact, but the solid is generated from the cissoid (meaning ‘ivy-shaped’). The canonical curve has equation
y
2
=
x
3
/(1 −
x
), which is shown in
figure 8.5
; evidently, it has a vertical asymptote at
x
= 1. It is attributed to Diocles in about 180 bc in connection with his attempt to duplicate the cube by geometrical methods and appears in Eutocius’s commentaries on Archimedes’
On the Sphere and the Cylinder
, wherein
the method of exhaustion
was developed. The solid concerned is contained between the rotation of the upper half of the cissoid and the vertical asymptote about the
y
-axis; it forms a goblet-shaped figure, as shown in
figure 8.6
.
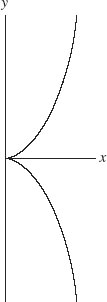
Figure 8.5.
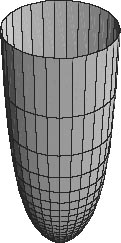
Figure 8.6.
The cissoid.
In a letter to Huygens, de Sluze mischievously described the solid as
a drinking glass that had small weight, but that even the hardiest drinker could not empty
(levi opera deducitur mensura vasculi, pondere non magni, quod interim helluo nullus ebibat).
Torricelli’s Trumpet would satisfy the more moderate drinker, but the glass could never be wetted! Admittedly, this is fanciful
for several important reasons, but the imagery is compelling. Where is the paradox? As ever, our senses have deceived us when we have brought about the confusion which arises when we try to bring to the real world something which cannot exist within it; infinitely long things cannot be brought into reality (Euclid’s parallels postulate reveals the danger in trying to do so) and wine is not infinitely thin.
Galileo’s own view echoes this:
[Paradoxes of the infinite arise] only when we attempt, with our finite minds, to discuss the infinite, assigning to it those properties which we give to the finite and limited.
But we should leave the last word to Hobbes, when he commented on the assertion that an infinite solid of finite volume exists:
To understand this for sense, it is not required that a man should be a geometrician or a logician, but that he should be mad.
NONTRANSITIVE EFFECTS
We want the surprise to be transitive like the impatient thump which unexpectedly restores the picture to the television set, or the electric shock which sets the fibrillating heart back to its proper rhythm.
Seamus Heaney
The Background
A dictionary definition of the adjective ‘transitive’ is ‘being or relating to a relationship with the property that if the relationship holds between a first element and a second and between the second element and a third, it holds between the first and third elements.’
Initially it is easy to imagine that all meaningful relationships between all pairs of objects are transitive: ‘older than’, ‘bigger than’, etc., but we do not need to look too far to produce examples for which transitivity fails: ‘son of’, ‘perpendicular to’, etc. This chapter is primarily concerned with a relationship which is seemingly transitive, but in fact need not be: that relationship is ‘better than’.
For example, suppose that A is a better tennis player than B and that B is a better tennis player than C, then it’s pretty clear
that A is a better tennis player than C; ‘better than’ is evidently transitive in this case.
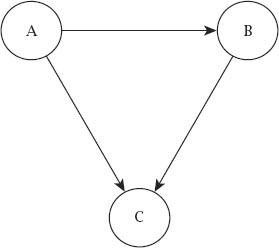
Figure 9.1.
A transitive relationship.
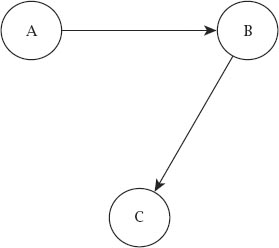
Figure 9.2.
Where transitivity is not defined.
If we represent a relationship between pairs of elements by ‘
→
’ and call the elements A, B and C, it will be transitive if
figure 9.1
holds.
With the two nontransitive relationships above, it is the case that the diagram simply cannot be completed and so becomes
figure 9.2
; A and C simply do not share the relationship of A with B and B with C.
Things become decidedly more confusing when the diagram completes to
figure 9.3
, where the arrows chase each other’s
tails; this is altogether stranger. In particular, how can it be that A is better than B, B is better than C and yet C is better than A?
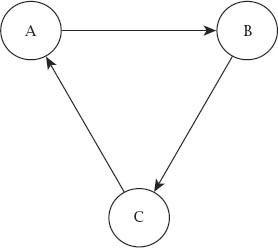
Figure 9.3.
Where transitivity is confounded.
Do such relationships exist? The answer is decidedly
yes
. A familiar example from childhood is the game of scissors–paper–rock, where each of two players holds a hand behind his or her back. On the count of three, both players bring their hidden hand forward in one of three configurations. Two fingers in a ‘V’ to represent scissors, the whole hand flat and slightly curved to represent paper, and a clenched fist to represent rock. The winner is determined by the following sequence of rules: scissors cut paper, paper wraps rock and rock breaks scissors, where ‘better than’ has an appropriate definition in each of the three cases. There is no ‘best’ choice and, with A representing ‘scissors’, B representing ‘rock’ and C representing ‘paper’, that tail-chasing is evident.
We will continue to more devious examples; in each case, ‘better than’ is given the specific interpretation ‘is more likely to win than’.
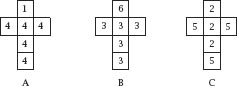
The Lo Shu Magic Square
The 4200-year-old Lo Shu magic square, shown in
figure 9.4
, provides the basis of the first example and one can be confident that the mathematicians of the time of Emperor Yu would have had no idea of this hidden property of the design. It is, of course, a
3
×
3 square with each of the nine squares filled with one of the integers from 1 to 9, the ‘magic’ stems from the fact that each row, column and diagonal add up to the magic number of 15.
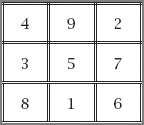
Figure 9.4.
The Lo Shu magic square.
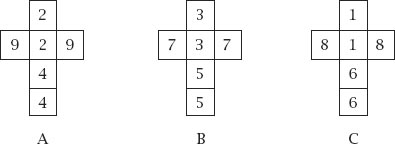
Figure 9.5.
The Lo Shu dice nets.
Now take the three rows and number three six-sided die each with two repeats of the three numbers forming each row, as shown by the nets of
figure 9.5
.
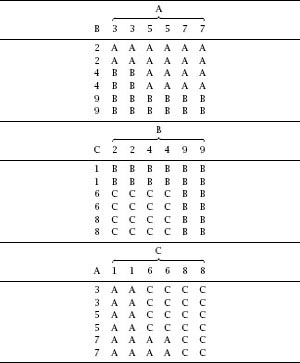
We can use these curiously numbered dice to play a simple game of chance with an opponent: he chooses a die, then we choose a die and we roll them (say) 100 times and see who wins the most times.
Table 9.1
lists the possible outcomes with each die matched against each, and shows that A → B → C → A, each with a probability of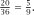 We have a situation which is modelled by
We have a situation which is modelled by
figure 9.3
, which means that, if we allow our opponent first choice of die, we will always be in the better position.
The choice of numbers is not unique. Toy collector and consultant Tim Rowett devised a set of three nontransitive dice where no face has a number higher than 6 (the highest number on a standard six-sided die);
figure 9.6
gives the nets. Again, A → B → C → A; in this case, the reader may wish to check that the probabilities of winning in each case are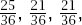 respectively.
respectively.
Table 9.1.
The Lo Shu dice compared.