Nonplussed! (21 page)
Authors: Julian Havil

If we look at the problem through modern eyes, taking the finite trumpet from
x
= 1 to
x
=
N
(forgetting the lip) and then allowing
N
to become arbitrarily large, we have that the volume of the trumpet is given by
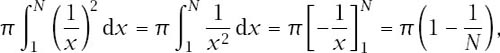
and as
N
→ ∞ the volume approaches
π
.
The simple calculation
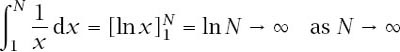
shows that we have a solid of infinite cross-sectional area but finite volume.
To calculate the surface area of the finite solid and so prove that it is also infinite requires more e3ort.
The Trumpet’s Surface Area
Using the standard formula for the surface area of a volume of revolution, as described in appendix C:
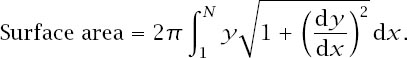
Here we have
y
= 1/
x
and so
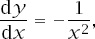
so the formula becomes
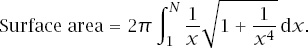
This clearly diverges since
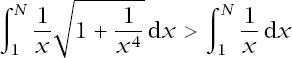
but it is pleasing, if a little messy, to find an exact form for the integral
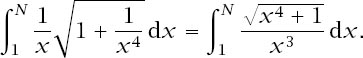
We will attack it in two stages: first using integration by parts and then substitution. So, with the indefinite integral:
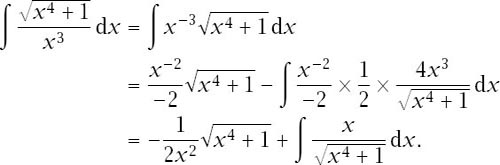
Now consider the remaining integral and use the substitution
u
=
x
2
, in which case d
u
/d
x
= 2
x
. We then have
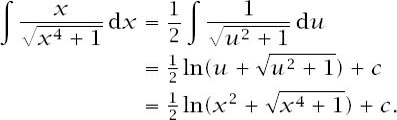
Putting all this together results in the surface area of the trumpet being given by
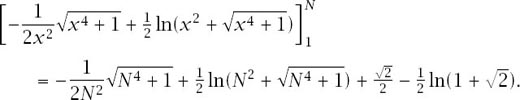
As
N
→ ∞ the first term clearly approaches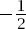 but the log function increases without bound, which means that the surface area also increases without bound.
but the log function increases without bound, which means that the surface area also increases without bound.
(It is appropriate that an anagram of ‘Evangelista Torricelli’ is ‘Lo! It is a clever integral’.)
The Trumpet’s Centre of Mass
The confusion is complete when we consider a comment of Wal-lis that a
surface, or solid, may be supposed to be so constituted, as to be Infinitely Long, but Finitely Great, (the Breadth
continually decreasing in greater proportion than the Length Increaseth,) and so as to have no Centre of Gravity. Such is Toricellio’s Solidum Hyperbolicum acutum.
Using the standard calculus definition of the centre of mass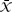 of a solid of revolution about the
of a solid of revolution about the
x
-axis, we have that