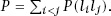Nonplussed! (19 page)

The fifth entry of
table 7.1
stands out. The final column would have us believe that
π
has been estimated to an accuracy of six
decimal places by the method, far in excess of the accuracy of the other entries: was it luck or deception?

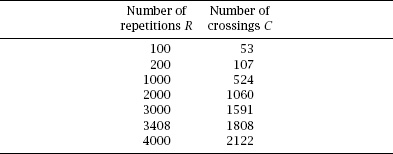
Table 7.2.
Lazzarini’s data.

In 1901 the Italian mathematician Mario Lazzarini published the result under the rather wordy title, ‘Un applicazione del calcolo della probabilità alla ricerca sperimentale di un valor approssimato di
π
’, in the journal
Periodico di Matematica
4:140–43; four pages of fame which has led to many more pages of suspicion and of outright rebuttal. Gridgeman’s article provided compelling reasons to doubt, the excellent 1965 book
Puzzles and Paradoxes
by Tim O’Beirne built on that doubt and Lee Badger’s analysis in ‘Lazzarini’s lucky approximation of
π
’ (
Mathematics Magazine
67(2), April 1994) pretty much signed the intellectual death warrant.

We will not attempt to discuss the matter at any length here, but a few details from these studies are hard to ignore. In fact, Lazzarini reported the data as part of a table of results of a number of such experiments, shown as
table 7.2
. We must conclude that he was a patient man.

Of course, it is that penultimate entry which stands out, initially because of the curious 3408 repetitions (of a needle with
l
= 2.5 cm tossed across parallel lines with
d
= 3 cm). What also stands out is that 3.141 592 9 is the seven-decimal-place approximation to the second-best-known rational approximation of
π
of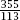
(known in the fifth century to Tsu Chung-chih).

Perhaps it was deception. If we follow Badger’s and O’Beirne’s reverse engineering, since 2
l
/(
πd
) ≈
R
/
C
it is the case that
2
Cl
/
dR
≈
π
and if we use our rational estimate for
π
we have that

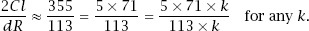
Table 7.3.
Empirical compared with theoretical data.

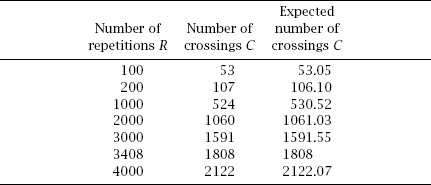
A reasonable choice is 2
l
= 5, which makes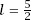
and since
d
>
l
a reasonable choice for that is
d
= 3 and this makes
C
/
R
= 213
k
/113
k
. Provided that
C
and
R
are chosen to make their ratio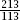
, the result will be achieved: with
k
= 16 we have Lazzarini’s figures.

Or it may have been luck. With 2
l
/
πd
≈
R
/
C
and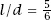
we have that 5/3
π
≈
R
/
C
and so
π
≈ 5
C
/3
R
. O’Beirne points out that one trial earlier than the given final repetition of
R
= 3408 would have
R
= 3407 and
C
= 1807 or
C
= 1808, which would make the estimate
π
≈ 3.142 … and
π
≈ 3.140 …, respectively, each out in the third decimal place. In turn, Badger points out that had there been
C
= 1807 or
C
= 1809 crossings in 3408 repetitions, the estimates would be
π
≈ 3.143 … and
π
≈ 3.139 …, respectively; the experiment does seem to have stopped on something of a cusp of luck.

Now consider the rest of the data. Again, with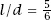
, the probability of a crossing is 2
l
/
πd
= 5/3
π
and so, on average, the expected number of crossings is (5/3
π
)×
R
and if we extend
table 7.2
to include these values we arrive at
table 7.3
.

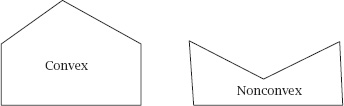
Figure 7.10.
Convexity and nonconvexity

It all looks too accurate and some simple statistical tests quantify that suspicion; the chances of this happening are less than 3 × 10
⁻⁵
. And this is our, but by no means Badger’s, final word on the topic.

A Generalization and a Final Surprise

Buffon mentioned throwing a square object: in fact, we can formulate a surprising result for any convex, polygonal lamina. First, a polygonal lamina is
convex
if it contains all line segments connecting all pairs of points on it. For example,
figure 7.10
shows a convex and a nonconvex pentagon.

Note that an immediate consequence of convexity is that any straight line will intersect precisely two sides of the lamina or none at all.

Now suppose that we throw the lamina onto a set of parallel, ruled lines a constant distance
d
apart. Suppose also that the lamina is made up of
n
sides of length
l
_i
for
i
= 1, 2,…,
n
, where each side is less than
d
. Since the order in which we count the sides is irrelevant, the intersection of a ruled line with the lamina must occur with the line pair (
l
_i
l
_j
) of the lamina for some pair
i
and
j
, where we may assume
i
<
j
, and suppose that this occurs with probability
P
(
l
_i
l
_j
). This means that the probability of an intersection of the lamina with a line is