Nonplussed! (20 page)

If the side
l
_i
is intersected with probability
P
(
l
_i
), since the lamina is convex, so must exactly one of the remaining sides, and so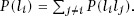
This means that

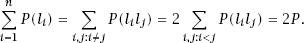
Now we use the previous result for Buffon’s Needle to write
P
(
l
_i
) = 2
l
_i
/
πd
and so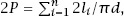
which makes

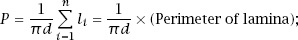
the probability that the lamina crosses a line is completely independent of its shape, depending only on its perimeter.

There are many more variants and generalizations of the original, novel idea of the eighteenth-century polymath Georges Louis Leclerc, Comte de Buffon: instead of parallel lines a rectangular grid, or perhaps radial lines or unequally spaced lines with a needle with a ‘preferred’ orientation (which is apparently useful in determining the spacing of flight lines for locating anomalies in airborne geophysical surveys). The Monte Carlo technique, of which this is the original example, is commonly used to estimate lengths of curves and areas of regions. In recent research on ants choosing nesting sites it has been suggested that the ant scouts’ critical job of site selection is influenced by estimates of area based on a variant of Buffon’s principle. Newton’s words have resonance:

Nature is pleased with simplicity, and affects not the pomp of superfluous causes.

But then, with so much needle tossing to do, so have those of Buffon himself:

Never think that God’s delays are God’s denials. Hold on; hold fast; hold out. Patience is genius!

TORRICELLI’S TRUMPET

The notion of infinity is our greatest friend; it is also the greatest enemy of our peace of mind.

James Pierpont

An Argument

One of the longest and most vitriolic intellectual disputes of all time took place between the two seventeenth-century luminaries Thomas Hobbes and John Wallis: Hobbes, the philosopher, had claimed to have ‘squared the circle’ and Wallis, the mathematician, had strongly and publicly refuted that claim.

This ancient problem (one of three of its kind) had been handed down by the Greeks and asked if it was possible, using straight edge and compasses only, to construct a square equal in area to the given circle: it took until 1882 until Ferdinand Lin-demann proved
π
to be transcendental, which meant that the question was resolved in the negative. Wallis was right.

Although the ‘squaring the circle’ problem spawned the conflict, the battle lines extended far beyond it – and in fact to the infinite, a concept which was far from understood at the time and which brought with it all manner of technical and philosophical
difficulties, and it is one particular example of infinity’s capricious nature that crystallized the adversaries’ opposing views of the concept: Torricelli’s Trumpet (or The Archangel Gabriel’s Trumpet, or Horn).

A Strange Trumpet

Bonaventura Cavalieri was a mathematician good enough to be praised by Galileo, who said of him, ‘few, if any, since Archimedes, have delved as far and as deep into the science of geometry’. And it was Archimedes’
method of exhaustion
which Cavalieri developed to form his theory of
indivisibles
, that is, finding lengths, areas and volumes by slicing the object in question into infinitesimally small pieces. To this he added
Cavalieri’s Principle
. This was 1629 and integral calculus was yet to be forged at the anvils of the yet unborn Newton and Leibniz; Cavalieri’s ideas would help with the process.

Evangelista Torricelli (remembered as the inventor of the barometer), frequent correspondent of Cavalieri and assistant to an ageing Galileo, was also an accomplished mathematician. Most particularly, using the method of
indivisibles
, in 1645 he
rectified
the Logarithmic Spiral (that is, he was able to measure the length of the curve; a result we will use in
chapter 10
).

Our interest lies with some of his earlier work when, in 1643, he had made known his discovery of the strange nature of the
acute hyperbolic solid
, which we would now call the rectangular hyperboloid. It is generated by rotating the rectangular hyperbola
y
= 1/
x
by 360° about the
x
-axis.
figure 8.1
shows the solid.

He showed that this infinite solid has a finite volume. To today’s post-calculus eyes this single fact is not shocking but it does become rather more surprising when we realize that not only is its length infinite, but so is its surface area.

We will use calculus and modern-day notation to prove both results: that the volume is finite and the surface area infinite. First, we will take the trouble to demonstrate Torricelli’s method of showing that the volume is finite, a result which shocked the thinkers of the day.

Torricelli’s Proof

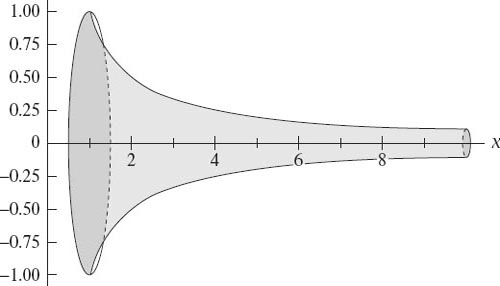
Figure 8.1.
Torricelli’s Trumpet

We have mentioned the term
Cavalieri’s Principle
. Archimedes had used the idea to find the volume of a sphere and a version of it can be stated in the following way:

Given two solids included between parallel planes, if every plane cross-section parallel to the given planes has areas in the same ratio in both solids, then the volumes of the solids are in that ratio.

In particular, if the areas of the sections are always equal, then so are the volumes.

The principle is deceptively powerful and before we discuss Torricelli’s use of it with the trumpet we will acclimatize ourselves to it by looking at a famous example of its use: computing the volume of a sphere (knowing the volume of a circular cone).

On the left of
figure 8.2
is a hemisphere of radius
r
with a horizontal section at height
h
above the base of the hemisphere. On the right is a cylinder of radius
r
and of height
r
with another horizontal section cut at height
h
above its base. Within the cylinder is inscribed a circular cone with base the top of the cylinder and vertex at the centre of the cylinder’s base. The area of the horizontal circular section within the hemisphere is
π
(
r
²
−
h
²
). Since the height of the cone at this level is
h
, so must be its base radius. This means that the area of the annular region within
the cylinder is
πr
²
−
πh
²
=
π
(
r
²
−
h
²
) also. Using Cavalieri’s Principle it must be that the volume of the hemisphere is equal to the volume of the cylinder minus the volume of the cone. We have, then, that the volume of the hemisphere is

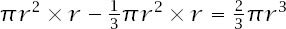
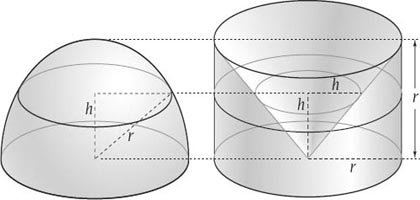
Figure 8.2.
Cavalieri’s Principle at work.

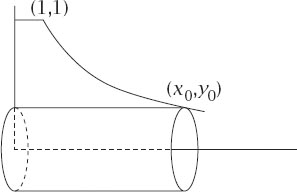
Figure 8.3.
Torricelli’s use of Cavalieri’s Principle which demonstrated the infinite volume.

and the volume of the sphere is

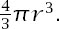
Torricelli used an extended form of the principle to show that the volume of the infinite trumpet is itself finite. To appreciate his proof we must imagine the trumpet to have a ‘lip’ at its open end and be made up of an infinite number of concentric, horizontal cylinders.
figure 8.3
shows a particular example of such a cylinder and let us suppose that the lip begins at the point (1,1).

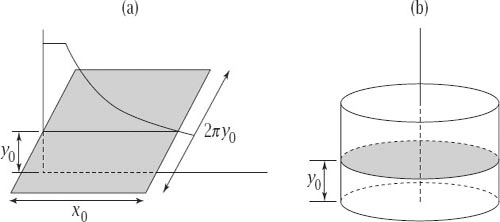
Figure 8.4.

Suppose now that the right end of a particular cylinder touches the hyperbola in the
xy
-plane at the point (
x
₀
,
y
₀
), then the cylinder has curved surface area (2
πy
₀
)
x
₀
= 2
πx
₀
y
₀
= 2
π
since
y
₀
= 1/
x
₀
. This area is, therefore, constant as the point of contact varies. Now unravel the cylinder so that it becomes a horizontal rectangle located at height
y
₀
, as shown in
figure 8.4
(a). Finally, construct a vertical cylinder made up of horizontal discs each of area 2
π
at height
y
₀
from its base, as shown in
figure 8.4
(b). The height of this cylinder will be 1. Cavalieri’s Principle is itself a limiting argument, if that is now extended to allow
x
₀
→ ∞ and so approach the base of the vertical cylinder, the volume of the trumpet is the same as the volume (2
π
) of that cylinder.

Of course, this argument is special. It works because
xy
= 1 and could not be easily extended to other cases, but it does work and it did shock. Torricelli himself said

It may seem incredible that although this solid has an infinite length, nevertheless none of the cylindrical surfaces we considered has an infinite length but all of them are finite.