Nonplussed! (25 page)
Authors: Julian Havil

The analysis is complete and we have established the nontransitivity.

A PURSUIT PROBLEM
This book is written in mathematical language and its characters are triangles, circles and other geometrical figures, without whose help… one wanders in vain through a dark labyrinth.
Galileo Galilei
The defunct magazine
Graham DIAL
was circulated to 25 000 American engineers during the 1940s and featured a
Private Corner for Mathematicians
, edited by L. A. Graham himself and populated by problems posed by readers for other readers to solve. Akin to Martin Gardner’s articles in
Scientific American
, the articles spawned two books which discussed, commented on and sometimes extended the original contributions. The first book,
Ingenious Mathematical Problems and Methods
, was published in 1959 and contains the problem we will discuss here. It is framed as a chase on the high seas, and does not seem to have sufficient information provided to be able to solve it. For its solution we will need two special curves, the nature of which we will deal with first.
A Linear Pursuit Curve

Figure 10.1.
A linear pursuit curve.
Pursuit curves were first studied in 1732 by the French scientist Pierre Bouguer, who was also the first person to measure the Earth’s magnetic field. Their exact nature depends on the path of the pursued and the method of pursuit, but the common ground is that they are the paths a pursuer should take when attempting to intercept a quarry.
Suppose that we assume the pursued to be moving in a straight line and that the pursuer always steers towards his quarry’s current position, continually altering course to achieve this. With this agreed, we arrive at the ‘linear pursuit curve’, solved by Arthur Bernhart, and which can be shown to have an equation of the form
y
=
cx
2
− ln
x
; it is shown in
figure 10.1
.
Pursuit Using the Circle of Apollonius
Alternatively, the pursuer could catch the quarry more quickly by utilizing a special plane curve: the Circle of Apollonius, named after Apollonius of Perga (ca. 262 b.c.e. to ca. 190 b.c.e.), which can be defined in the following way.
Take two distinct fixed points
A
and
B
and consider the set of all points
P
such that
PA
:
PB
=
k
for some positive constant
k
. If
k
= 1, the points form the perpendicular bisector of
AB
, otherwise they form a circle, the Circle of Apollonius, as shown in
figure 10.2
.
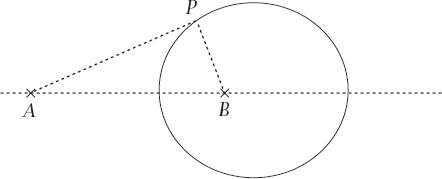
Figure 10.2.
The circle of Apollonius.
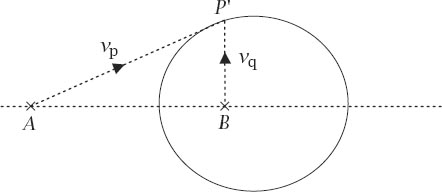
Figure 10.3.
A certain capture.
Now suppose that the speed of the pursuer is
υ
p
and that of the quarry is
υ
q
and that at some point the pursuer is at position
A
and the quarry at position
B
. Given that the pursuer knows
υ
q
, he should mentally construct the Circle of Apollonius as the set of points
P
such that
AP
:
PB
=
υ
p
:
υ
q
, as shown in
figure 10.3
. Given also that the pursuer knows the direction of flight, he will be able to calculate the point
P
′ at which the pursued will cross the circle. He should head for
P
′ and so ensure capture at that point.
The Circle of Apollonius will not be suffcient in itself for the solution to our problem, but it will have its contribution to make.
Pursuit Using the Logarithmic Spiral
A pleasing generalization of a pursuit curve results from taking several objects, each one acting as pursuer and quarry. For example, in
figure 10.4
we imagine four spiders, each starting at a corner of a square and moving with equal, constant speed toward one another. In
figure 10.5
lines have been drawn linking
some of the positions of pursuer and quarry and the diagram becomes a work of mathematical art.
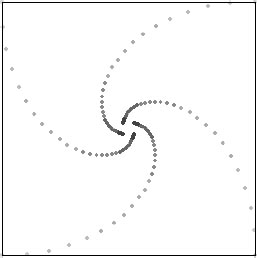
Figure 10.4.
Four spiders in mutual pursuit.
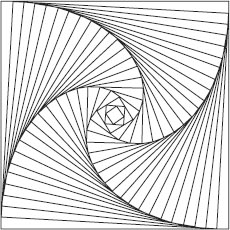
Figure 10.5.
Four spiders with some links.
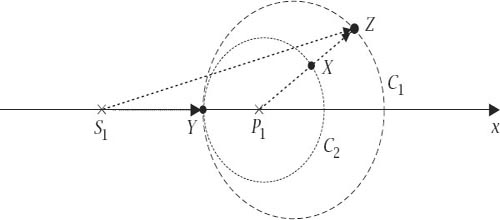
Figure 10.6.
A logarithmic spiral.
These last, artistically satisfying, examples trace self-similar curves known as
logarithmic
(or equiangular)
spirals
, whose polar equation is
r
=
a
e
bθ
for constants
a
and
b
. A typical example is shown in
figure 10.6
. They were first studied in 1638 by
René Descartes but are most famously associated with Jakob Bernoulli, who developed many of their startling properties. So enamoured of them was he that he asked for one to be engraved on his tombstone with the phrase ‘Eadem mutata resurgo’ (‘I shall arise the same, though changed’); unfortunately, the stonemason seems to have been unduly challenged by the charge and produced a somewhat crude Archimedean Spiral (whose polar form is
r
=
aθ
). An essential difference between the two spirals is that successive turnings of the Archimedean Spiral have a constant separation distance (of 2
πa
), whereas with the logarithmic spiral these distances are in geometric progression.
Logarithmic spirals abound in nature: they are the paths along which insects approach a light source and hawks approach their prey, the shape of spiral galaxies (including our own Milky Way) and also of cyclones. In Book 1 of
Principia
Newton proved that if the universal law of gravitation had been an inverse cubic law, rather than our familiar square law, a possible orbit of the planets around the Sun would have been that of a logarithmic spiral.
Logarithmic spirals are remarkable curves for very many reasons, and one will prove to be the second curve needed for the solution to our principal problem.
Before we do so, it is impossible to ignore an amusing anecdote relating to the remarkable analytic number theorist G. H. Hardy, in which he posits an equation which represents an equiangular spiral, which is also a parabola, and a hyperbola.
During his tenure of the Savilian Chair of Geometry at Oxford, he gave his presidential address to the Mathematical Association in 1925, under the title, ‘What is geometry?’, in the course of which he said with characteristic clarity:
You might object…that geometry is, after all, the business of geometers, and that I know, and you know, and I know that you know, that I am not one; and that it is useless for me to try to tell you what geometry is, because I simply do not know. And here I am afraid that we are confronted with a regrettable but quite definite cleavage of opinion. I do not claim to know any geometry, but I do claim to understand quite clearly what geometry is.
He had, however, contributed to the geometrical literature with the following note, published in the
Mathematical Gazette
in 1907.
224
. [M
1
.8.g.]
A curious imaginary curve.
The curve (
x
+ i
y
)
2
= λ(
x
− i
y
) is (i) a parabola, (ii) a rectangular hyperbola, and (iii) an equiangular spiral. The first two statements are evidently true. The polar equation is
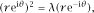
the equation of an equiangular spiral. The intrinsic equation is easily found to be
ρ
= 3i
s
.
It is instructive (i) to show that the equation of any curve which is both a parabola and a rectangular hyperbola can be put in the form given above, or in the form
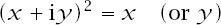
and (ii) to determine the intrinsic equation directly from one of the latter forms of the Cartesian equation.
G. H. Hardy
