Statistics Essentials For Dummies (28 page)

You can also use a confidence interval for one population mean to analyze the average difference in paired data from one population. For example, suppose you want to estimate the average effect of a certain drug on blood pressure. You take one sample of patients, measure their blood pressure before and after taking the drug, and record the differences in blood pressure. (This type of experiment is called a
matched-pairs design
; see Chapter 13.) These differences represent a single sample from a single population, so a confidence interval for one population mean can be used to estimate the average difference in blood pressure due to the drug.
Confidence Interval for a Population Proportion
When a characteristic being measured is categorical — for example, opinion on an issue (support, oppose, or are neutral), or type of behavior (do/don't wear a seatbelt while driving), people often want to estimate the proportion (or percentage) of people in the population that fall into a certain category of interest. Examples include the percentage of people in favor of a four-day work week, or the proportion of drivers who don't wear seat belts. In each of these cases, the object is to estimate a population proportion using a sample proportion plus or minus a margin of error. The result is called a
confidence interval for a population proportion, p.
The formula for a CI for a population proportion,
p
, is
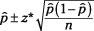
where
is the sample proportion;
n
is the sample size; and
z*
is the appropriate value from the standard normal (
Z
-) distribution for your desired confidence level. (Note that a
sample proportion
is the proportion of individuals in the sample that had the characteristic of interest.)
For example, suppose you want to estimate the percentage of the time you get a red light at a certain intersection. If you want a 95% confidence interval, your
z*-
value is 1.96. You take a random sample of 100 different trips through this intersection, and you find that you hit a red light 53 times, so= 53/100 = 0.53. Take 0.53 times (1 - 0.53) and divide by 100 to get 0.249/100 = 0.00249.Take the square root to get 0.0499 or 0.05. The margin of error is, therefore, plus or minus 1.96 * 0.05 = 0.098.
Your 95% confidence interval for the percentage of times you will ever hit a red light at that particular intersection is 0.53 (or 53%) plus or minus 0.098. The lower end of the interval is 0.530 - 0.098 = 0.43 or 43%; the upper end is 0.530 + 0.098 = 0.63 or 63%.) You conclude the overall percentage of the times you should expect to hit a red light at this intersection is somewhere between 43% and 63%, based on your sample, with a confidence level of 95%.
Confidence Interval for the Difference of Two Means
The goal of many surveys and medical studies is to compare two populations, such as males versus females or Republicans versus Democrats. When the characteristic being compared is numerical (for example, height, weight, or income) the object of interest is the amount of difference in the means (averages) for the two populations. For example, you may want to compare the difference in average age of Republicans versus Democrats, or the difference in average incomes of men versus women. You estimate the difference between two population means by taking a sample from each population and using the difference of the two sample means, plus or minus a margin of error. The result is a
confidence interval for the difference of two population means,.
The formula for a CI for the difference between two population means is
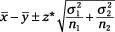
where
and
are the sample means, respectively;
n
1
and
n
2
are the sample sizes;and
are the population standard deviations; and
z*
is the appropriate value from the standard normal (
Z
-) distribution for your desired confidence level (see Table 7-1 for values of
z*
for certain confidence levels).
