Gödel, Escher, Bach: An Eternal Golden Braid (57 page)
Read Gödel, Escher, Bach: An Eternal Golden Braid Online
Authors: Douglas R. Hofstadter
Tags: #Computers, #Art, #Classical, #Symmetry, #Bach; Johann Sebastian, #Individual Artists, #Science, #Science & Technology, #Philosophy, #General, #Metamathematics, #Intelligence (AI) & Semantics, #G'odel; Kurt, #Music, #Logic, #Biography & Autobiography, #Mathematics, #Genres & Styles, #Artificial Intelligence, #Escher; M. C

We can dignify this observation by calling it the
Central Dogma of MIathematical
Logic
, and depicting it in a two-step diagram:
TNT
=>
N
=> meta-
'TNT
In words: a string of
TNT
has an interpretation in N; and a statement o may have a second meaning as a statement about
TNT
.
G
: A String Which Talks about Itself in Code
This much is intriguing yet it is only half the story. The rest of the st involves an intensification of the self-reference. We are now at the st where the Tortoise was when he realized that a record could be m; which would make the phonograph playing it break-but now the quest is: "Given a record player, how do you actually figure out what to put the record?" That is a tricky matter.
We want to find a string of TNT-which we'll call 'G'-which is ab itself, in the sense that one of its passive meanings is a sentence about G. particular the passive meaning will turn out to be
"
G
is not a theorem of
TNT
."
I should quickly add that
G
also has a passive meaning which is a sta
tement of number
theory;
just like
MUMON
it is susceptible to being construed in least) two different ways. The important thing is that each passive mean is valid and useful and doesn't cast doubt on the other passive meaning in any way. (The fact that a phonograph playing a record can induce vibrations in itself and in the record does not diminish in any way the fact t those vibrations are musical sounds!)
G's Existence Is What Causes TNT's Incompleteness
The ingenious method of creating
G
, and some important concepts relating to
TNT
, will be developed in Chapters XIII and XIV; for now it is interesting to glance ahead, a bit superficially, at the consequences finding a self-referential piece of
TNT
. Who knows? It might blow up! In a sense it does. We focus down on the obvious question: Is
G
a theorem of
TNT
, or not?
Let us be sure to form our
own
opinion on this matter, rather than rely G's opinion about itself. After all, G may not understand itself any be than a Zen master understands himself. Like
MUMON
,
G
may express a falsity. Like
MU
,
G
may be a nontheorem. We don't need to believe every possible string of
TNT
-only its theorems. Now let us use our power of reasoning to clarify the issue as best we can at this point.
We will make our usual assumption: that
TNT
incorporates valid methods of reasoning, and therefore that
TNT
never has falsities for theorems. In other words, anything which is a theorem of
TNT
expresses a truth. So if
G
were a theorem, it would express a truth, namely: "
G
is not a theorem". The full force of its self-reference hits us. By being a theorem,
G
would have to be a falsity. Relying on our assumption that
TNT
never has falsities for theorems, we'd be forced to conclude that
G
is
not a theorem
.
This is all right; it leaves us, however, with a lesser problem. Knowing that
G
is not a theorem, we'd have to concede that
G
expresses a truth. Here is a situation in which
TNT
doesn't live up to our expectations-we have found a string which expresses a true statement yet the string is not a theorem. And in our amazement, we shouldn't lose track of the fact that
G
has an arithmetical interpretation, too-which allows us to summarize our findings this way:
A string of
TNT
has been found; it expresses, unambiguously, a statement about certain arithmetical properties of natural numbers; moreover, by reasoning outside the system we can determine not only that the statement is a true one, but also that the string fails to be a theorem of
TNT
. And thus, if we ask
TNT
whether the statement is true,
TNT
says neither yes nor no.
Is the Tortoise's string in the
Mu Offering
the analogue of
G
? Not quite. The analogue of the Tortoise's string is
~G.
Why is this so? Well, let us think a moment about what -G says. It must say the opposite of what
G
says.
G
says, "
G
is not a theorem of
TNT
", so
~G
must say "
G
is a theorem". We could rephrase both
G
and
~G
this way:
G
: "I am not a theorem (of
TNT
)."
~G
: "My negation is a theorem (of
TNT
)."
It is
~G
which is parallel to the Tortoise's string, for that string spoke not about itself, but about the string which the Tortoise first proffered to Achilles -- which had an extra knot on it (or one too few, however you want to look at it).
Mumon Has the Last Word
Mumon penetrated into the Mystery of the Undecidable anyone, in his concise poem on Joshu's MU:
Has a dog Buddha-nature?
This is the most serious question of all.
If you say yes or no,
You lose your own Buddha-nature.
Prelude . .
Achilles and the Tortoise have come to the residence of their friend the Crab, to
make the acquaintance of one of his friends, the Anteater. The introductions
having been made, the four of them settle down to tea.
Tortoise We have brought along a little something for you, Mr. Crab. Crab: That's most kind of you. But you shouldn't have.
Tortoise: Just a token of our esteem. Achilles, would you like to give it to Mr. C?
Achilles: Surely. Best wishes, Mr. Crab. I hope you enjoy it.
(Achilles hands the Crab an elegantly wrapped present, square and very thin. The
Crab begins unwrapping it.)
Anteater: I wonder what it could be.
Crab: We'll soon find out. (Completes
the unwrapping, and pulls out the gif)t
Two records! How exciting! But there's no label. Uh-oh-is this another of your "specials", Mr. T?
Tortoise: If you mean a phonograph-breaker, not this time. But it is in fact a custom-recorded item, the only one of its kind in the entire world. In fact, it's never even been heard before-except, of course, when Bach played it.
Crab: When Bach played it? What do you mean, exactly?
Achilles: Oh, you are going to be fabulously excited, Mr. Crab, when Mr. T tells you what these records in fact are.
Tortoise: Oh, you go ahead and tell him, Achilles.
Achilles: May I? Oh, boy! I'd better consult my notes, then. (P
ulls out a small filing card,
and clears his voice
.) Ahem. Would you be interested in hearing about the remarkable new result in mathematics, to which your records owe their existence?
Crab: My records derive from some piece of mathematics? How curious Well, now that you've provoked my interest, I must hear about it.
Achilles: Very well, then. (
Pauses for a moment to sip his tea, then resumes)
Have you heard of Fermat's infamous "Last Theorem"?
Anteater: I'm not sure ... It sounds strangely familiar, and yet I can't qui place it.
Achilles: It's a very simple idea. Pierre de Fermat, a lawyer by vocation b mathematician by avocation, had been reading in his copy of the class text
Arithmetica
by Diophantus, and came across a page containing the equation
a2+b2=c2
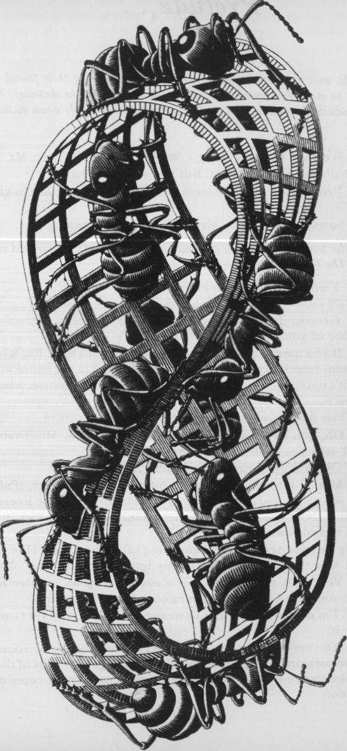
FIGURE 54. Mobius Strip II, by M. C. Escher (woodcut, 1963).
He immediately realized that this equation has infinitely many solutions a, b, c, and then wrote in the margin the following notorious comment:
The equation
an +bn=cn
has solutions in positive integers a, b, c, and n only when n = 2 (an then there are infinitely many triplets a, b, c which satisfy the equation); but there are no solutions for n > 2. I have discovered a truly marvelous proof of this statement, which, unfortunately, this margin is too small to contain.
Ever since that day, some three hundred years ago, mathematicians have been vainly trying to do one of two things: either to I Fermat's claim, and thereby vindicate Fermat's reputation, whit though very high, has been somewhat tarnished by skeptics who he never really found the proof he claimed to have found-or e: refute the claim, by finding a counterexample: a set of four integers a, b, c, and n, with n > 2, which satisfy the equation. Until recently, every attempt in either direction had met with failure. 1 sure, the Theorem has been proven for many specific values of i particular, all n up to 125,000.
Anteater: Shouldn't it be called a "Conjecture" rather than a "Theorem it's never been given a proper proof?
Achilles: Strictly speaking, you're right, but tradition has kept it this i Crab: Has someone at last managed to resolve this celebrated quest Achilles: Indeed! In fact, Mr. Tortoise has done so, and as usual, by a wizardly stroke. He has not only found a PROOF of Fermat's Theorem (thus justifying its name as well as vindicating Fermat; also a COUNTEREXAMPLE, thus showing that the skeptics had good intuition!
Crab: Oh my gracious! That is a revolutionary discovery.
Anteater: But please don't leave us in suspense. What magical integer they, that satisfy Fermat's equation? I'm especially curious about the value of n.
Achilles: Oh, horrors! I'm most embarrassed! Can you believe this? the values at home on a truly colossal piece of paper. Unfortunately was too huge to bring along. I wish I had them here to show to y( it's of any help to you, I do remember one thing-the value of n only positive integer which does not occur anywhere in the continued fraction for
π
Crab: Oh, what a shame that you don't have them here. But there reason to doubt what you have told us.

FIGURE 55. Pierre de Fermat.
Anteater: Anyway, who needs to see n written out decimally? Achilles has just told us how to find it. Well, Mr. T, please accept my hearty felicitations, on the occasion of your epoch-making discovery!
Tortoise: Thank you. But what I feel is more important than the result itself is the practical use to which my result immediately led.
Crab: I am dying to hear about it, since I always thought number theory was the Queen of Mathematics -- the purest branch of mathematic -- the one branch of mathematics which has No applications!
Tortoise: You're not the only one with that belief, but in fact it is quite impossible to make a blanket statement about when or how some branch-or even some individual Theorem-of pure mathematics will have important repercussions outside of mathematics. It is quite unpredictable-and this case is a perfect example of that phenomenon.
Achilles: Mr. Tortoise's double-barreled result has created a breakthrough in the field of acoustico-retrieval!
Anteater: What is acoustico-retrieval?
Achilles: The name tells it all: it is the retrieval of acoustic information from extremely complex sources. A typical task of acoustico-retrieval is to reconstruct the sound which a rock made on plummeting into a lake from the ripples which spread out over the lake's surface.
Crab: Why, that sounds next to impossible!
Achilles: Not so. It is actually quite similar to what one's brain does, when it reconstructs the sound made in the vocal cords of another person from the vibrations transmitted by the eardrum to the fibers in the cochlea.
Crab: I see. But I still don't see where number theory enters the picture, or what this all has to do with my new records.
