The Singularity Is Near: When Humans Transcend Biology (15 page)
Read The Singularity Is Near: When Humans Transcend Biology Online
Authors: Ray Kurzweil
Tags: #Non-Fiction, #Fringe Science, #Retail, #Technology, #Amazon.com

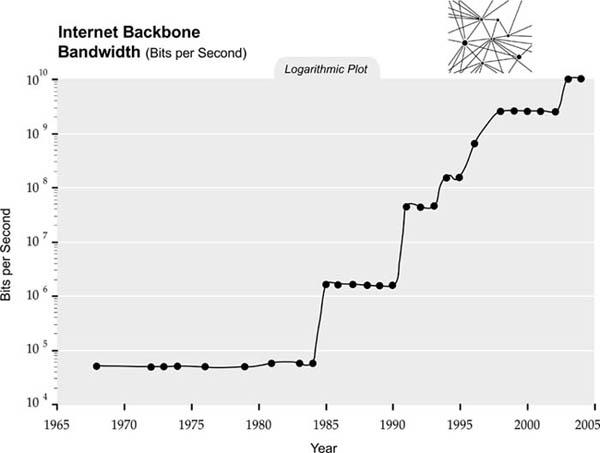
Another trend that will have profound implications for the twenty-first century is the pervasive movement toward miniaturization. The key feature sizes of a broad range of technologies, both electronic and mechanical, are decreasing, and at an exponential rate. At present, we are shrinking technology by a factor of about four per linear dimension per decade. This miniaturization is a driving force behind Moore’s Law, but it’s also reflected in the size of all electronic systems—for example, magnetic storage. We also see this decrease in the size of mechanical devices, as the figure on the size of mechanical devices illustrates.
54
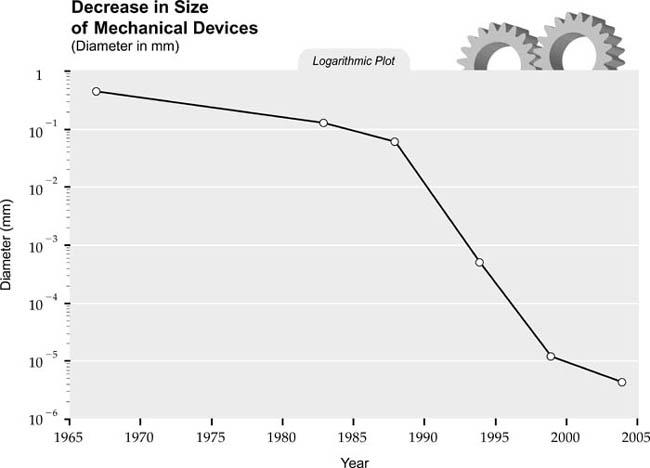
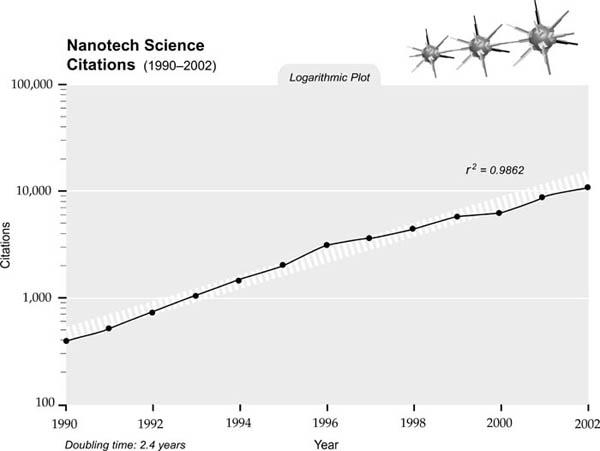
As the salient feature size of a wide range of technologies moves inexorably closer to the multinanometer range (less than one hundred nanometers—billionths of a meter), it has been accompanied by a rapidly growing interest in nanotechnology. Nanotechnology science citations have been increasing significantly over the past decade, as noted in the figure below.
55
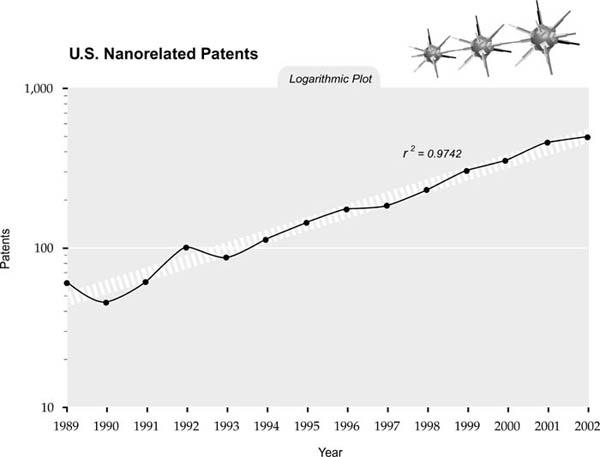
We see the same phenomenon in nanotechnology-related patents (below).
56
As we will explore in
chapter 5
, the genetics (or biotechnology) revolution is bringing the information revolution, with its exponentially increasing capacity and price-performance, to the field of biology. Similarly, the nanotechnology revolution will bring the rapidly increasing mastery of information to materials and mechanical systems. The robotics (or “strong AI”) revolution involves the reverse engineering of the human brain, which means coming to understand human intelligence in information terms and then combining the resulting insights with increasingly powerful computational platforms. Thus, all three of the overlapping transformations—genetics, nanotechnology, and robotics—that will dominate the first half of this century represent different facets of the information revolution.
Information, Order, and Evolution:
The Insights from Wolfram and Fredkin’s Cellular Automata
As I’ve described in this chapter, every aspect of information and information technology is growing at an exponential pace. Inherent in our expectation of a Singularity taking place in human history is the pervasive importance of information to the future of human experience. We see information at every level of existence. Every form of human knowledge and artistic expression—scientific and engineering ideas and designs, literature, music, pictures, movies—can be expressed as digital information.
Our brains also operate digitally, through discrete firings of our neurons. The wiring of our interneuronal connections can be digitally described, and the design of our brains is specified by a surprisingly small digital genetic code.
57
Indeed, all of biology operates through linear sequences of 2-bit DNA base pairs, which in turn control the sequencing of only twenty amino acids in proteins. Molecules form discrete arrangements of atoms. The carbon atom, with its four positions for establishing molecular connections, is particularly adept at creating a variety of three-dimensional shapes, which accounts for its central role in both biology and technology. Within the atom, electrons take on discrete energy levels. Other subatomic particles, such as protons, comprise discrete numbers of valence quarks.
Although the formulas of quantum mechanics are expressed in terms of both continuous fields and discrete levels, we do know that continuous levels can be expressed to any desired degree of accuracy using binary data.
58
In fact, quantum mechanics, as the word “quantum” implies, is based on discrete values.
Physicist-mathematician Stephen Wolfram provides extensive evidence to show how increasing complexity can originate from a universe that is at its core a deterministic, algorithmic system (a system based on fixed rules with predetermined outcomes). In his book
A New Kind of Science
, Wolfram offers a comprehensive analysis of how the processes underlying a mathematical construction called “a cellular automaton” have the potential to describe every level of our natural world.
59
(A cellular automaton is a simple computational mechanism that, for example, changes the color of each cell on a grid based on the color of adjacent or nearby cells according to a transformation rule.)
In his view, it is feasible to express all information processes in terms of operations on cellular automata, so Wolfram’s insights bear on several key issues related to information and its pervasiveness. Wolfram postulates
that the universe itself is a giant cellular-automaton computer. In his hypothesis there is a digital basis for apparently analog phenomena (such as motion and time) and for formulas in physics, and we can model our understanding of physics as the simple transformations of a cellular automaton.
Others have proposed this possibility. Richard Feynman wondered about it in considering the relationship of information to matter and energy. Norbert Wiener heralded a fundamental change in focus from energy to information in his 1948 book
Cybernetics
and suggested that the transformation of information, not energy, was the fundamental building block of the universe.
60
Perhaps the first to postulate that the universe is being computed on a digital computer was Konrad Zuse in 1967.
61
Zuse is best known as the inventor of the first working programmable computer, which he developed from 1935 to 1941.
An enthusiastic proponent of an information-based theory of physics was Edward Fredkin, who in the early 1980s proposed a “new theory of physics” founded on the idea that the universe is ultimately composed of software. We should not think of reality as consisting of particles and forces, according to Fredkin, but rather as bits of data modified according to computation rules.
Fredkin was quoted by Robert Wright in the 1980s as saying,
There are three great philosophical questions. What is life? What is consciousness and thinking and memory and all that? And how does the universe work? . . . [The] “informational viewpoint” encompasses all three. . . . What I’m saying is that at the most basic level of complexity an information process runs what we think of as physics. At the much higher level of complexity, life, DNA—you know, the biochemical functions—are controlled by a digital information process. Then, at another level, our thought processes are basically information processing. . . . I find the supporting evidence for my beliefs in ten thousand different places. . . . And to me it’s just totally overwhelming. It’s like there’s an animal I want to find. I’ve found his footprints. I’ve found his droppings. I’ve found the half-chewed food. I find pieces of his fur, and so on. In every case it fits one kind of animal, and it’s not like any animal anyone’s ever seen. People say, Where is this animal? I say, Well, he was here, he’s about this big, this that, and the other. And I know a thousand things about him. I don’t have him in hand, but I know he’s there. . . . What I see is so compelling that it can’t be a creature of my imagination.
62
In commenting on Fredkin’s theory of digital physics, Wright writes,
Fredkin . . . is talking about an interesting characteristic of some computer programs, including many cellular automata: there is no shortcut to finding out what they will lead to. This, indeed, is a basic difference between the “analytical” approach associated with traditional mathematics, including differential equations, and the “computational” approach associated with algorithms. You can predict a future state of a system susceptible to the analytic approach without figuring out what states it will occupy between now and then, but in the case of many cellular automata, you must go through all the intermediate states to find out what the end will be like: there is no way to know the future except to watch it unfold. . . . Fredkin explains: “There is no way to know the answer to some question any faster than what’s going on.” . . . Fredkin believes that the universe is very literally a computer and that it is being used by someone, or something, to solve a problem. It sounds like a good-news/bad-news joke: the good news is that our lives have purpose; the bad news is that their purpose is to help some remote hacker estimate pi to nine jillion decimal places.
63
Fredkin went on to show that although energy is needed for information storage and retrieval, we can arbitrarily reduce the energy required to perform any particular example of information processing, and that this operation has no lower limit.
64
That implies that information rather than matter and energy may be regarded as the more fundamental reality.
65
I will return to Fredkin’s insight regarding the extreme lower limit of energy required for computation and communication in
chapter 3
, since it pertains to the ultimate power of intelligence in the universe.
Wolfram builds his theory primarily on a single, unified insight. The discovery that has so excited Wolfram is a simple rule he calls cellular automata rule 110 and its behavior. (There are some other interesting automata rules, but rule 110 makes the point well enough.) Most of Wolfram’s analyses deal with the simplest possible cellular automata, specifically those that involve just a one-dimensional line of cells, two possible colors (black and white), and rules based only on the two immediately adjacent cells. For each transformation, the color of a cell depends only on its own previous color and that of the cell on the left and the cell on the right. Thus, there are eight possible input situations (that is, three combinations of two colors). Each rule maps all combinations of these eight input situations to an output (black or white). So there are 2
8
(256) possible rules for such a one-dimensional, two-color, adjacent-cell automaton. Half of the 256 possible rules map onto the other half because of left-right symmetry. We can map half of them again because of black-white equivalence, so we are left with 64 rule types. Wolfram illustrates the action of these automata with two-dimensional patterns in which each line (along the
y
-axis) represents a subsequent generation of applying the rule to each cell in that line.
Most of the rules are degenerate, meaning they create repetitive patterns of no interest, such as cells of a single color, or a checkerboard pattern. Wolfram calls these rules class 1 automata. Some rules produce arbitrarily spaced streaks that remain stable, and Wolfram classifies these as belonging to class 2. Class 3 rules are a bit more interesting, in that recognizable features (such as triangles) appear in the resulting pattern in an essentially random order.
However, it was class 4 automata that gave rise to the “aha” experience that resulted in Wolfram’s devoting a decade to the topic. The class 4 automata, of which rule 110 is the quintessential example, produce surprisingly complex patterns that do not repeat themselves. We see in them artifacts such as lines at various angles, aggregations of triangles, and other interesting configurations. The resulting pattern, however, is neither regular nor completely random; it appears to have some order but is never predictable.
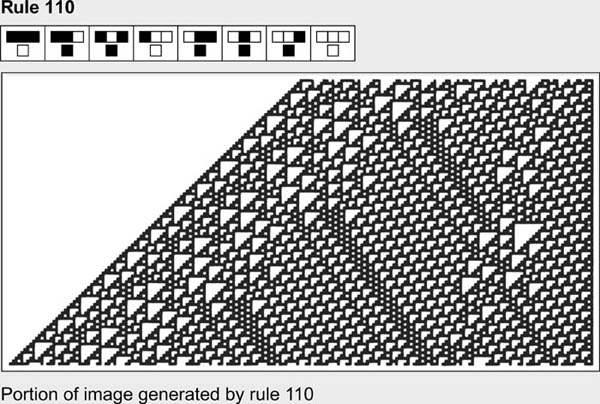
Why is this important or interesting? Keep in mind that we began with the simplest possible starting point: a single black cell. The process involves repetitive application of a very simple rule.
66
From such a repetitive and deterministic process, one would expect repetitive and predictable behavior. There are two surprising results here. One is that the results produce apparent randomness. However, the results are more interesting than pure randomness, which itself would become boring very quickly. There are discernible and interesting features in the designs produced, so the pattern has some order and apparent intelligence. Wolfram includes a number of examples of these images, many of which are rather lovely to look at.
Wolfram makes the following point repeatedly: “Whenever a phenomenon is encountered that seems complex it is taken almost for granted that the phenomenon must be the result of some underlying mechanism that is itself complex. But my discovery that simple programs can produce great complexity makes it clear that this is not in fact correct.”
67
I do find the behavior of rule 110 rather delightful. Furthermore, the idea that a completely deterministic process can produce results that are completely unpredictable is of great importance, as it provides an explanation for how the world can be inherently unpredictable while still based on fully deterministic rules.
68
However, I am not entirely surprised by the idea that simple mechanisms can produce results more complicated than their starting conditions. We’ve seen this phenomenon in fractals, chaos and complexity theory, and self-organizing systems (such as neural nets and Markov models), which start with simple networks but organize themselves to produce apparently intelligent behavior.
At a different level, we see it in the human brain itself, which starts with only about thirty to one hundred million bytes of specification in the compressed genome yet ends up with a complexity that is about a billion times greater.
69
It is also not surprising that a deterministic process can produce apparently random results. We have had random-number generators (for example, the “randomize” function in Wolfram’s program Mathematica) that use deterministic processes to produce sequences that pass statistical tests for randomness. These programs date back to the earliest days of computer software, such as the first versions of Fortran. However, Wolfram does provide a thorough theoretical foundation for this observation.
Wolfram goes on to describe how simple computational mechanisms can exist in nature at different levels, and he shows that these simple and deterministic mechanisms can produce all of the complexity that we see and experience. He provides myriad examples, such as the pleasing
designs of pigmentation on animals, the shape and markings of shells, and patterns of turbulence (such as the behavior of smoke in the air). He makes the point that computation is essentially simple and ubiquitous. The repetitive application of simple computational transformations, according to Wolfram, is the true source of complexity in the world.
My own view is that this is only partly correct. I agree with Wolfram that computation is all around us, and that some of the patterns we see are created by the equivalent of cellular automata. But a key issue to ask is this:
Just how complex are the results of class 4 automata?
Wolfram effectively sidesteps the issue of degrees of complexity. I agree that a degenerate pattern such as a chessboard has no complexity. Wolfram also acknowledges that mere randomness does not represent complexity either, because pure randomness also becomes predictable in its pure lack of predictability. It is true that the interesting features of class 4 automata are neither repeating nor purely random, so I would agree that they are more complex than the results produced by other classes of automata.
